Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.1 - Ex. 49
Encontre os valores de máximo e mínimo absoluto de no intervalo dado
Passo 1
Olá, meu nobre amigo. Yuri aqui e estarei te ajudando a resolver essa atividade. Aqui deveremos encontrar os pontos máximos e mínimos da função dada no intervalo dado.
Os pontos críticos de uma função são os valores de nos quais a derivada da função é igual a zero ou não está definida.
Primeiramente, necessitamos calcular a derivada de para encontrar os números críticos.
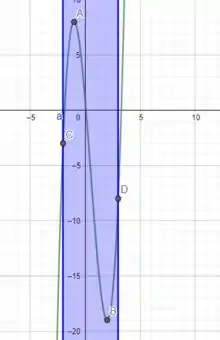
Acima vemos o gráfico da nossa função no intervalo dado.
Passo 2
Então, a derivada da função é:
Igualando a zero
Usando a formula de Baskara iremos encontrar os zeros da função, ficamos com
Passo 3
Agora, aplicando o método do intervalo fechado, pois é continua no intervalo dado, necessitamos calcular e .
A primeira condição para encontramos o numero critico já fizemos, que era encontrar os zeros para a derivada.
A segunda condição é localizar os valores nos pontos finais do intervalo.
Os pontos de extremidade do intervalo são e . Então, nós substuimos e na equação .
A terceira condição é encontrarmos o maior e o menor valor no passo anterior, o maior valor é e menor . Sendo assim, o máximo absoluto é em , por ‘produzir’ o maior valor e o mínimo absoluto é em por ‘produzir’ o valor menor valor.
Resposta
é um ponto de máximo absoluto e é um ponto de mínimo absoluto