Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 4.Exercícios Práticos - Ex. 13a
Um gráfico que seja grande o suficiente para mostrar o comportamento global de uma função pode deixar de revelar aspectos locais importantes. O gráfico de é um desses casos.
a. Faça o gráfico de no intervalo . Onde o gráfico parece ter valores extremos locais ou pontos de inflexão?
Passo 1
Fazendo o esboço do gráfico dessa função dada, tem-se:
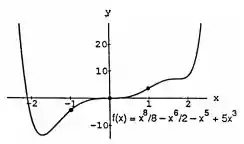
Observando o desenho acima, é possível encontrar dois mínimos locais: e , sendo que o primeiro ponto aparentemente é um máximo absoluto.
Além disso, existem pontos de inflexão (onde a função muda a sua concavidade) em , e .
Resposta
a. Mínimos locais: e ;
Pontos de inflexão: e .
Exercícios de Livros Relacionados
Prove que:Seja c um ponto crítico de uma função f , no qual f ' c = 0 e suponhamos que f ' exista para todos os valores de x em algum intervalo aberto contendo c . Se f ' ' c existe eSe f ' ' c0 , ent
Suponha que f seja uma função para o qual f ' ' x existe para todos os valores de x num intervalo aberto I e que para um número c em I , f ' ' c = 0 e f ' ' ' c existe e não é zero. Prove que o ponto
Ache os extremos absolutos da função dada no intervalo indicado, se existir algum. f x = x + 2 x - 2 - 4,4
Ache os extremos absolutos da função dada no intervalo indicado, se existir algum. f x = x 3 - 3 x + 5 - ∞ , 0
Ache os extremos absolutos da função dada no intervalo indicado, se existir algum. f x = x 3 + 2 x 2 - 4 x + 1 - 3,2