Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 5.1 - Ex. 3b
Repita a parte (a) usando extremos esquerdos.
Passo 1
Oie, vamos dar continuidade a resolução.
No passo a) dividimos em subtintervalos, calculamos o
e então utilizamos a soma:
Isso é, utilizamos a altura do inicio de cada retângulo. Lembre-se que nossa função é a:
E o nosso intervalo é:
Agora fazemos o mesmo que no item (a), porém pegamos como altura dos retângulos a função no início de cada intervalo. Nossos retângulos então ficam assim:
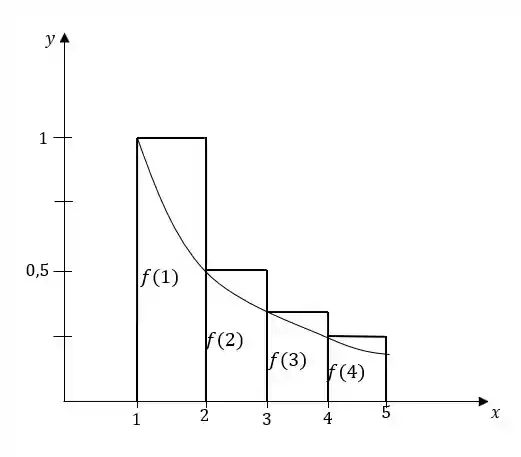
Passo 2
Então fazemos o cálculo da soma das áreas dos retângulos:
Pela figura, podemos ver que a área real sob a curva é menor que a que calculamos, então nosso resultado é uma superestimativa.
Resposta
Exercícios de Livros Relacionados
Use a Regra do Trapézio e os dados a seguir para estimar o valor da integral ∫ 0 3,2 f x d x .Se soubermos que - 4 ≤ f ' x ≤ 1 para todo x , estime o erro envolvido na aproximação da parte (a).
A tabela dá o consumo de potência em megawatts, em Ontário, da meia-noite até às 6 horas da manhã em 10 de dezembro de 2004 . Use a Regra de Simpson para estimar a energia usada durante aquele período
O gráfico a seguir mostra o tráfego de dados em um provedor de serviços na Internet entre meia-noite e as 8 horas da manhã. D denota os dados em processamento, medidos em megabits por segundo. Use a R
Estime a área sob o gráfico na figura usando (a) a Regra do Trapézio, (b) a Regra do Ponto Médio e (c) a Regra de Simpson, cada qual com n = 6 .
Ache as aproximações T n , M n e S n para n = 6 e 12 . Então calcule os erros correspondentes E T , E M e E S . (Arredonde seu resultado para seis casas decimais. Você pode usar o comando soma em um s