Há uma boa chance de que um CAS não seja capaz de calcular a integral dada. Se for esse o caso, faça uma substituição de forma a obter uma integral que seu CAS possa calcular.
Passo 1
Como a gente é curioso, vamos tentar descobrir que substituição é essa que deixa essa integral mais fácil para o nosso programinha.
Vamos reescrever essa integral:
Repara que temos um produto de funções dentro do quadrado e temos um termo do lado de fora que parece muito uma regra do produto.
A gente pode tentar usar a substituição:
E usando a regra do produto:
Olha só! Apareceu exatamente o termo do lado de fora da raiz quando achamos . Então essa é a substituição que vamos usar.
Passo 2
Aplicando essa substituição na nossa integral, temos que:
Ficou uma integral bem mais bonitinha, né? Vamos jogar no Wolfram Mathematica:
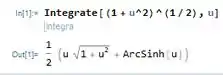
E lembrando que :
Que lindo! Conseguimos!