O projeto do Gateway Arch em St. Louis, Missouri, foi elaborado pelo arquiteto Eero Saarinan e implementado usando as equações fornecidas pelo Dr. Hannskarl Badel. As equações usadas para curva central do arco foram
com entre e .
(a) Use um recurso computacional para fazer o gráfico da curva central do arco.
(b) Encontre o comprimento da curva central com quatro casas decimais.
(c) Para quais valores de a altura do arco é ? Arredonde sua resposta para quatro casas decimais.
(d) Aproxime até o grau mais próximo o ângulo agudo que a reta tangente à curva central faz com o solo no final do arco.
Passo 1
(a) Vamos usar a calculadora gráfica do Geogebra (dá para acessar pelo navegador), para esboçar essa curva, no intervalo dado.
Fica assim:
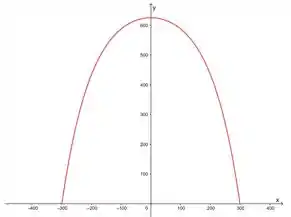
Passo 2
(b) A fórmula para o comprimento da curva, no intervalo , é:
Para o nosso caso, os dados ficam:
E pela regra da cadeia:
Substituindo esses dados na fórmulinha, e calculando a integral na calculadora gráfica, a gente tem que:

Passo 3
(c) A altura do arco é o valor de . Então precisamos descobrir para que valores de temos , usando a equação do arco:
Substituindo e isolando :
Fazendo essa continha na calculadora:
Lembrando que a gente coloca esse porque o cosseno hiperbólico é uma função par (simétrica em relação ao eixo ).
Passo 4
(d) Sabemos que o ângulo que uma reta faz com a horizontal é:
Onde é o coeficiente angular da reta.
E sabemos também que o coeficiente angular da reta tangente à curva no ponto em que ela toca o chão, no final do arco é:
Onde
Podemos achar esse ângulo para o ponto final da curva, usando a expressão abaixo na calculadora gráfica:
O ângulo agudo é o ângulo, menor que , que a nossa reta faz com o eixo (solo). Pelo nosso resultado, a gente vê que esse ângulo é .
Resposta
(a) 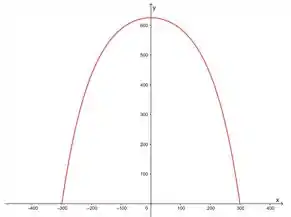
(b)
(c)
(d)