Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 3.5 - Ex. 57
A hipotenusa de um triângulo retângulo mede exatamente 10 cm, e um dos ângulos agudos mede , com erro possível de
(a) Use diferenciais para estimar os erros nos lados opostos e adjacente ao ângulo medido.
(b) Estime os erros percentuais nos lados.
Passo 1
Se x for o valor exato do ângulo e y a medida do lado estudado do triângulo, para o calculo do tamanho do lado teremos:
Lembrando que admitimos 10 cm como o valor da hipotenusa, sem nenhuma chance de erro sobre essa medida.
Se for o erro da medição, então o erro propagado pode ser aproximado por
Passo 2
Aplicando isso temos que:
Substituindo o valor medido do ângulo (30 ) nessa equação, e aplicando o erro de medida que está entre ficamos com:
Passo 3
Para o lado adjacente fazemos o mesmo, mas agora, ao invés de usarmos o lado com 30 usamos o de 60.
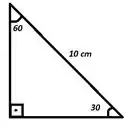
Substituindo o valor medido do ângulo (60 ) nessa equação, e aplicando o erro de medida que está entre ficamos com:
Passo 4
(b) Para a letra b precisamos estimar os erros percentuais dos lados.
Para o erro percentual do lado oposto temos sua media sendo 5cm, uma vez que , com erro de logo temos:
Já para o erro percentual do lado adjascente teremos como medida do lado , uma vez que . Seu erro calculamos como sendo de
Ficaremos então com: