Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 8.2 - Ex. 38
Um homem em um cais está puxando um bote por uma corda a uma velocidade de . As mãos do homem estão acima do ponto em que a corda está amarrada no bote. Com que velocidade estará variando o ângulo formado entre a corda e a superfície da água quando restarem para ser puxados de corda?
Passo 1
Um barco é puxado por uma corda a uma taxa constante de e a elevação da corda com relação à água é de , como ilustra a figura:
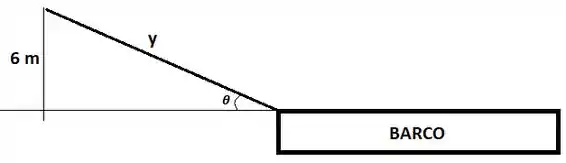
Queremos saber com que velocidade o ângulo varia, isto é, o valor de quando . Para isso, do triângulo retângulo, temos que
Precisamos derivar essa equação com relação ao tempo para obter .
Passo 2
Derivando com relação ao tempo:
Assim,
Agora basta substituir e . O sinal de menos no vem porque o comprimento da corda está diminuindo a uma taxa de . Assim,
Assim, a velocidade com o ângulo varia é