Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.5 - Ex. 73
Obtenha os gráficos das funções dadas em uma mesma tela. Como esses gráficos estão relacionados?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente esboçar os gráficos das funções , e , no intervalo , e explicar como esses gráficos estão relacionados.
Para isso, precisamos lembrar que a função seno é uma função trigonométrica e periódica, cujo gráfico é dado da seguinte forma:
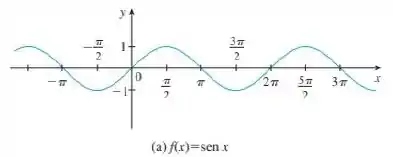
E que a função é a inversa da função , no intervalo . Mas por que nesse intervalo? Porque a função seno só será injetora se restringirmos o seu domínio e para que uma função tenha inversa, ela precisa ser injetora. Então, garantimos que a função seja invertível nesse intervalo.
Além disso, lembre-se que é uma reta crescente cujo coeficiente angular é , então ela “corta” o plano cartesiano na diagonal.
De posse dessas informações, vamos plotar as três curvas no plano e analisar a figura obtida para verificar a relação entre elas.
Vamos lá!
Passo 2
Esboçando os gráficos no intervalo dado, ficamos com:
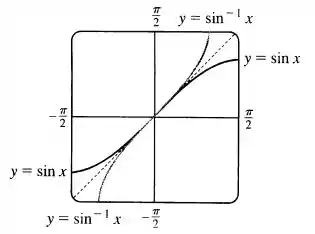
Observe que é como se a tivesse feito um zoom na função seno do passo , pegando só o pedaço onde vai de até , e depois refletisse essa curva em torno da reta .
Então, pelo gráfico, podemos ver que é a reflexão do gráfico em torno da reta . Assim, se , é o número entre e cujo seno é .
Valeu, galera! Até a próxima! 😉
Resposta
é a reflexão do gráfico em torno de