Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 16.6 - Ex. 16

Faça uma correspondência entre as equações e os gráficos identificados por I - V I e justifique sua resposta. Determine quais famílias de curvas da grade têm u constante e quais têm v constante.

x = 1 - u 3 + c o s   v   c o s   4 π u   ,

y = 1 - u 3 + c o s   v   s e n   4 π u   ,

z = 3 u + 1 - u s e n   v  

Passo 1

Iai pessoal, beleza???

Essa questão quer que a gente encontre o gráfico que corresponderá as equações:

x = 1 - u 3 + c o s   v   c o s   4 π u   ,

y = 1 - u 3 + c o s   v   s e n   4 π u   ,

z = 3 u + 1 - u s e n   v  

E depois determine quais famílias de curva da grade terão u constante e quais terão v constante.

Para isso vamos precisar avaliar como ficarão as equações quando u for em diferentes valores.

Juntando essas informações seremos capazes de achar o gráfico correspondente.

Passo 2

Vamos começar colocando u constante, como é uma constante podemos adotar um valor para ele. Vamos dizer que   u = 0   para facilitar as contas :

para x   :

→ x = 1 - u 3 + c o s   v   c o s   4 π u  

x = 1 - 0 3 + c o s   v   c o s   ( 4 π . 0 )  

x = 1 - 0 3 + c o s   v   c o s   ( 0 )  

Fazendo a distributiva:

x = 3   +   c o s   v    

para y   :

→ y = 1 - u 3 + c o s   v   s e n   4 π u   ,

y = 1 - 0 3 + c o s   v   s e n   4 π 0  

y = 0

para z   :

→ z = 3 u + 1 - u s e n   v  

→ z = 3.0 + 1 - 0 s e n   v  

z = s e n   v  

Logo podemos afirmar que são as equações de um círculo com raio igual a 1 no plano x z centrada em ( 3,0 , 0 ) .Se desenharmos graficamente acharemos:

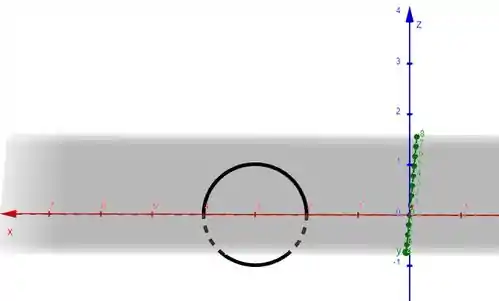
Passo 3

Agora vamos dizer que u = 1 2 :

→ x = 1 - u 3 + c o s   v   c o s   4 π u  

x = 1 - 1 2 3 + c o s   v   c o s   ( 4 π . 1 2 )  

x = 1 - 1 2 3 + c o s   v   c o s   ( 2 π )  

x = 1 - 1 2 3 + c o s   v   . 1  

Fazendo a distributiva:

x = 3 2   + 1 2 c o s   v    

para y   :

→ y = 1 - u 3 + c o s   v   s e n   4 π u   ,

y = 1 - 1 2 3 + c o s   v   s e n   ( 4 π . 1 2 )  

y = 1 - 1 2 3 + c o s   v   . 0  

y = 0

para z   :

→ z = 3 u + 1 - u s e n   v  

→ z = 3 . 1 2 + 1 - 1 2 s e n   v  

z = 3 2 + 1 2 s e n   v  

Essas são as equações de um círculo de raio 1 / 2 no plano x z centrada em 3 2 , 0 , 3 2 . Vamos ver gráficamente:

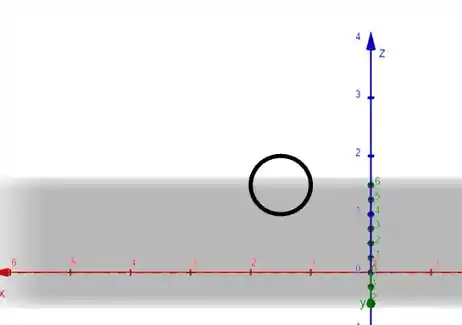
Passo 4

Por último vamos fazer u = 1 :

→ x = 1 - u 3 + c o s   v   c o s   4 π u  

x = 1 - 1 3 + c o s   v   c o s   ( 4 π . 1 )  

x = 0 3 + c o s   v   c o s   ( 2 π )  

x = 0  

para y   :

→ y = 1 - u 3 + c o s   v   s e n   4 π u   ,

y = 1 - 1 3 + c o s   v   s e n   ( 4 π . 1 )  

y = 0 3 + c o s   v   . 0  

y = 0

para z   :

→ z = 3 u + 1 - u s e n   v  

z = 3.1 + 1 - 1 s e n   v  

z = 3.1 + 0 s e n   v  

z = 3  

Essas são as equações de u

Logo, x = y = 0 e z = 3 , resultando no ponto mais alto na superfície. Ou seja, 0 , 0,3 .

Passo 5

Se juntarmos as curvas que encontramos podemos dizer que com v constante, temos uma forma espiral. que as curvas de grade com u constante são círculos orientados verticalmente visíveis.

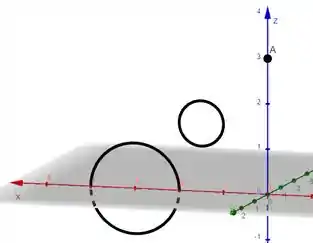
As curvas que nos achamos:

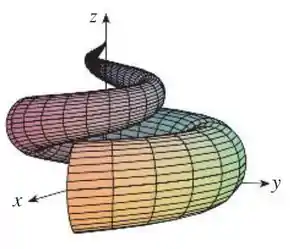
Olha como se assemelha a figura V.

Assim, o gráfico correspondente é o V !

Resposta

Gráfico V.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine uma representação paramétrica para a superfície.A parte do hiperboloide 4 x 2 - 4 y 2 - z 2 = 4 que está em frente ao plano y z .
Determine uma representação paramétrica para a superfície.O Plano que passa pelo ponto 0 , - 1,5 e contém os vetores 2,1 , 4 e - 3,2 , 5
Determine uma representação paramétrica para a superfície.A parte do elipsoide x 2 + 2 y 2 + 3 z 2 = 1 que se encontra à esquerda do plano x z .
Determine uma representação paramétrica para a superfície.O Plano que passa pela origem e contém os vetores i ^ - j ^ e j ^ - k ^
Determine se os pontos PeQ estão na superfície dada. r u , v = u + v ,u - 2 v , 3 + u - v P 4 , - 5,1 , Q ( 0,4 , 6 )