Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.8 - Ex. 7

Identifique a superfície com a equação dada.

ρ cos ⁡ ϕ = 1

Passo 1

Faaala galerinha, beleza?? Bora lá iniciar!!!

Bem, o enunciado forneceu uma expressão e pediu para determinar a superfície.

ρ cos ⁡ ϕ = 1

Tá, mas como eu faço isso?

Vamos pensar juntos, beleza?

Olhe bem para a expressão dada, e veja como é uma nomenclatura típica de coordenadas esféricas.

Já temos um caminho, então vamos estruturar ele.

Como é coordenadas esféricas. Bom, pegamos um ponto P na esfera, e descremos as coordenadas x , y e z :

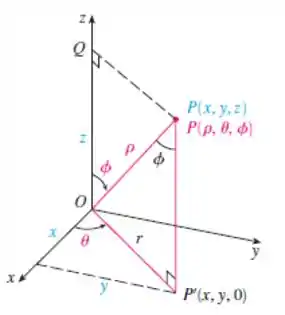
Das equações de transformação para coordenadas esféricas, temos:

x 2 + y 2 + z 2 = ρ 2

x = ρ s e n   ϕ cos ⁡ θ

y = ρ s e n   ϕ   s e n   θ

z = ρ cos ⁡ ϕ

Com essas informações, nosso objetivo é fazer o caminho inverso. Vamos achar uma relação da expressão dada com as expressões em coordenadas esféricas.

Vamos nessa então!!!

Passo 2

Vamos começar comparando a expressão dada com as expressões de coordenadas esféricas.

A expressão dada:

ρ c o s ϕ = 1

Em coordenadas esféricas temos:

x 2 + y 2 + z 2 = ρ 2

x = ρ s e n   ϕ cos ⁡ θ

y = ρ s e n   ϕ   s e n   θ

z = ρ cos ⁡ ϕ

Repare que a expressão dada é exatamente a componente z . Logo temos que:

ρ c o s ϕ = 1 = z

Dessa forma, podemos concluir que a equação representa o plano z = 1 .

Resposta

A equação representa o plano z = 1 .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a massa da bola B dada por x 2 + y 2 + z 2 ≤ a 2 se a densidade em qualquer ponto for proporcional à sua distância do eixo z.
Calcule a integral, transformando para coordenadas cilíndricas. ∫ - 2 2 ∫ - 4 - y 2 4 - y 2 ∫ x 2 + y 2 2 x z d z d x d y
Quando estudam a formação de cordilheiras, os geólogos estimam a quantidade de trabalho necessária para erguer uma montanha a partir do nível do mar. Considere uma montanha que tenha essencialmente o
Determine a massa e o centro de massa do sólido S limitado pelo paraboloide z = 4 x 2 + 4 y 2 e pelo plano z = a ( a0 ) , se S tem densidade constante K.
Calcule as integrais triplas abaixo, usando uma mudança de variáveis conveniente. ∫ ∫ ∫ W x 2 + y 2 + z 2 1 / 2 d x d y d z Onde W é a região dada por: i )W = x ,y ,z ∈ R 3|x 2 + y 2 + z 2 ≤ a 2 i i )