Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.6 - Ex. 16
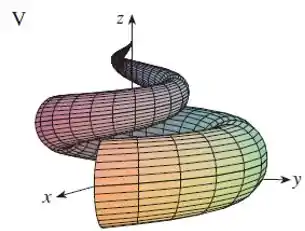
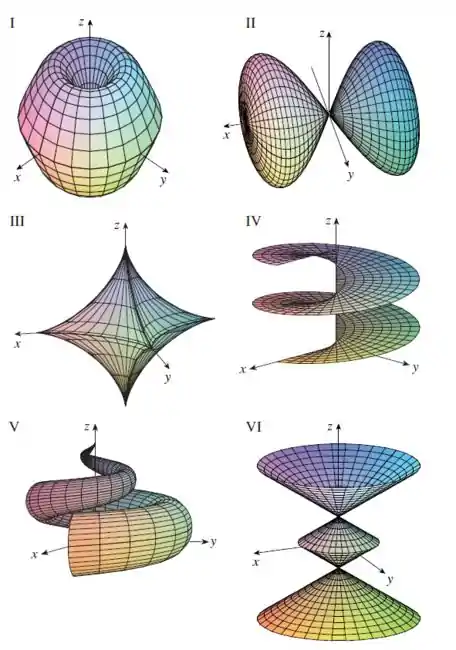
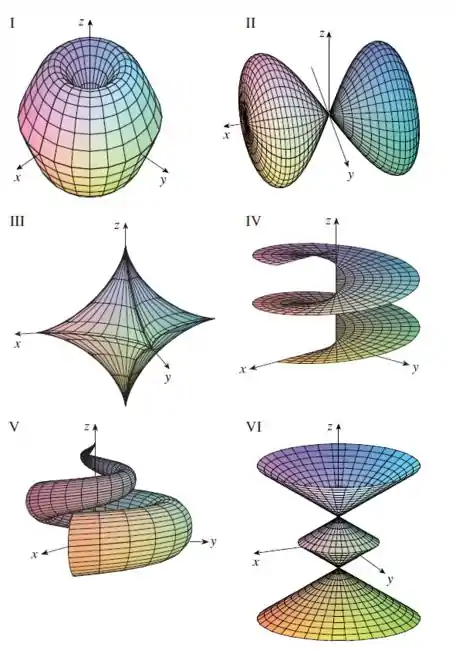
Faça uma correspondência entre as equações e os gráficos identificados por e justifique sua resposta. Determine quais famílias de curvas da grade têm constante e quais têm constante.
Passo 1
E aiii galera, tudo bem com vocês!?
Nessa questão temos que fazer a correspondência entre as imagens e a parametrização abaixo, assim como, determinar quais famílias de curvas da grade têm constante e quais têm constante.
Vamos com calma, que essa é mais complicadinha! Temos uma parametrização bem extensa!
Olhando as parametrizações:
O segredo para você identificar qual figura essa parametrização representa, é adotar alguns valores de u constante e verificar o comportamento da curva.
Eu quero que você adote os seguintes valores de :
Você deve substituir cada um desses valores na parametrização e então avaliar a curva que pode ser gerada pela expressão resultante.
Bora lá fazer isso!
Passo 2
Lembrando nossa parametrização, que é:
Vamos adotar alguns valores de constante para entender o comportamento das regiões.
Assim, as famílias de curvas da grade para:
Temos,
Essa parametrização corresponde a uma circunferência de raio no plano com centro .
Para,
Temos,
Que também corresponde a uma circunferência de raio no plano com centro .
Por fim, para:
Vamos ter:
Observe que para esse último valor de , temos o ponto mais alto do gráfico.
Olhando todos os gráficos o que melhor corresponde com a nossa analise é o gráfico , que mostra curvas de grade em espiral.
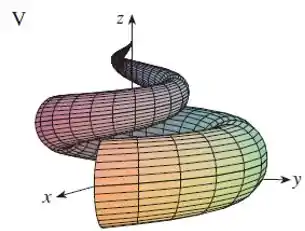
Passo 3
Para comprovar a escolha do gráfico , vamos utilizar o Geogebra 3D para plotar nossa parametrização.
Fazendo,
Logo, temos o gráfico:
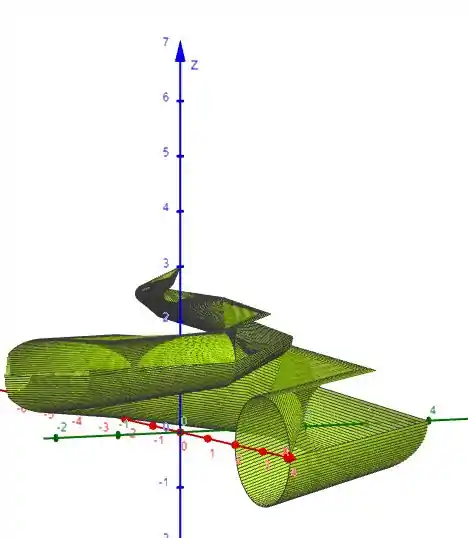
Você pode fazer utilizando o seguinte input no Geogebra 3D:
a=Superfície((1-u) (3+cos(v)) cos(4 π u),(1-u) (3+cos(v)) sen(4 π u),3 u+(1-u) sen(v),u,0,1,v,0,2 π)
Veja que a figura acima é exatamente igual ao gráfico .
Resposta
Gráfico
