Enunciado
Cálculo - Cálculo Volume 2 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 16.6 - Ex. 14
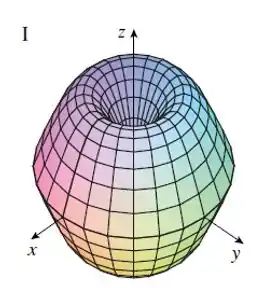
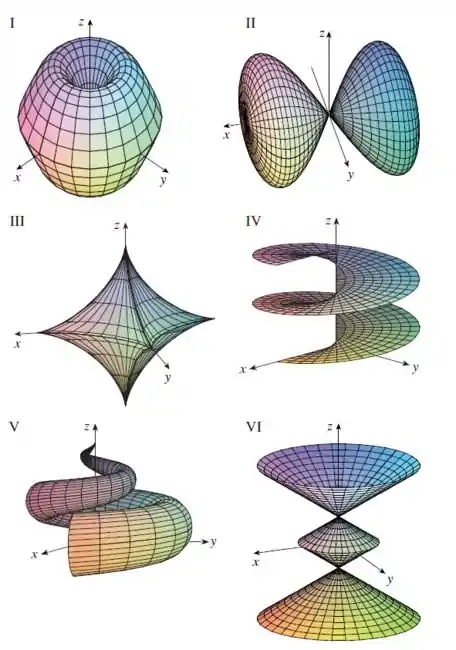
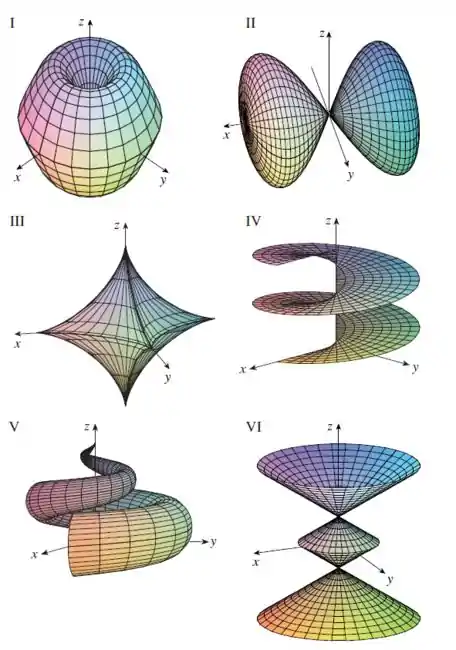
Faça uma correspondência entre as equações e os gráficos identificados por I-VI e justifique sua resposta. Determine quais famílias de curvas da grade têm constante e quais têm constante.
Passo 1
Faaaaala turma, beleza!?
Nessa questão temos que fazer uma correspondência entre as imagens e a parametrização:
E também, determinar quais famílias de curvas da grade têm constante e quais têm constante.
Vamos lá então!
Começando avaliando a equação paramétrica, temos que:
Com,
E agora? Você deve associar essa parametrização com a de um círculo em coordenadas polares.
Repare que no plano , temos uma parametrização típica de um círculo.
Sabendo disso, quero que você faça essa comparação. Aí você vai compreender que temos um círculo de raio no plano que está variando no intervalo de , e z também está limitado por uma curva senoidal entre:
Bora lá resolver essa!!
Passo 2
Vamos recapitular o que vimos. As equações paramétricas correspondem a:
No plano vamos ter vários círculos entre , e observe que se olharmos em cum plano ou a superfície tem a curva senoidal. Com isso, podemos ver que o gráfico I tem esse formato.
Vamos olhar as famílias de curvas da grade, isso ajuda a compreender o gráfico também.
Com constante:
Então temos curvas de grade no plano vertical no eixo .
Com constante, temos uma projeção circular no plano .
Como e são constantes múltiplas de e , cada um deles é uma onda senoidal, assim a superfície corresponde ao gráfico I.
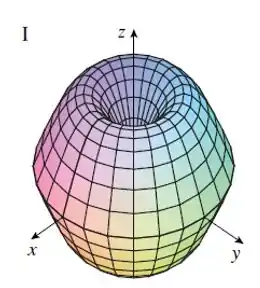
Resposta
Gráfico I
