Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.7 - Ex. 53
A iluminação de um objeto por uma fonte de luz é diretamente proporcional à potência ao quadrado da distância da fonte. Se duas fontes de luz, uma três vezes mais que a outra, são colocadas a de distância, onde deve ser colocado o objeto sobre a reta entre as fontes de forma a receber o mínimo de iluminação?
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente o local onde deve ser colocado o objeto sobre a reta entre duas fontes de luz de forma a receber o mínimo de iluminação. Pra isso, nós sabemos que a iluminação de um objeto por uma fonte de luz é diretamente proporcional à potência ao quadrado da distância da fonte.
Além disso, nós sabemos que essas fontes são colocadas a metros de distância uma da outra e que uma delas é três vezes mais forte que a outra. Como não sabemos a intensidade de cada uma, vamos chamar uma de e a outra de . Assim, o esboço do enunciado fica assim:
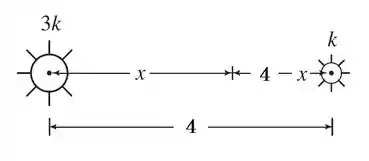
Então devemos encontrar uma expressão para essa iluminação em função da distância e minimizar essa função, através da derivação e de seus pontos críticos.
Vamos lá!
Passo 2
“A iluminação de um objeto por uma fonte de luz é diretamente proporcional à potência ao quadrado da distância da fonte.” Traduzindo essa frase temos a seguinte fórmula:
Onde , que é a distância total.
Passo 3
Agora para minimizar , vamos começar derivando a nossa função. Sendo:
Sua derivada será calculada usando a regra do expoente e a regra da cadeia, assim:
Como queremos achar o ponto onde a intensidade é mínima, basta igualar essa derivada a zero, e teremos:
Que pode ser escrita como:
E multiplicando cruzado, encontramos:
Simplificando , teremos:
Tirando a raiz cúbica nos dois lados:
Fazendo a distributiva,
E isolando o , teremos:
Colocando em evidência:
Esse número está entre e , então o objeto deve ser colocado a uma distância de da fonte de maior iluminação e a da fonte de menor iluminação.
Valeu, galera! Até a próxima! 😉
Resposta
Deve ser colocado a da fonte de maior iluminação, e a da fonte de menor iluminação.