Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.3 - Ex. 7
O Imposto de Renda dos EUA usa um sistema de depreciação linear de 10 anos para determinar o valor de vários itens comerciais. Isso significa que se supõe que um item tenha valor zero no final do décimo ano e que, em tempos intermediários, o valor é uma função linear do tempo decorrido. Esboce algumas retas de depreciação típicas e explique o significado prático do corte com o eixo y.
Passo 1
Bom, se o valor antes de anos é dado por uma reta, vamos ter uma função do tipo:
Onde será o tempo em anos (ou seja, só teremos valores positivos para , pois não existe tempo negativo) e é o valor do item (não teremos valores negativos para , pois não temos valores negativos de preço).
Além disso, queremos que, após anos, o valor seja , ou seja, queremos que passe pelo ponto . Substituindo isso na reta:
Ou seja, qualquer reta que obedeça a essa relação servirá para a depreciação vista no problema.
Passo 2
Esboçando algumas dessas retas:
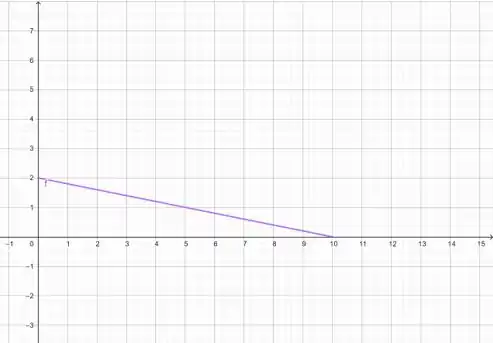
Mais umazinha:
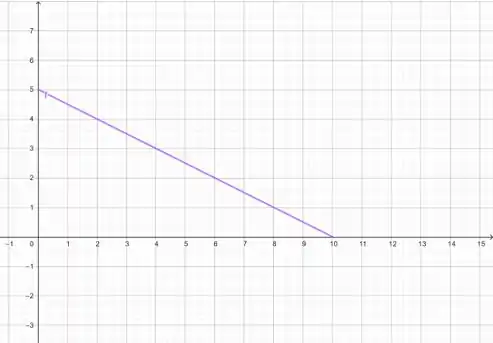
Como queríamos, os valores zeram após .
Passo 3
Se você reparar na equação:
O valor de (que é o corte com o eixo ) é achado quando . Dessa forma, isso significa que representa o valor do item no tempo , ou seja, o valor inicial do item!
Resposta
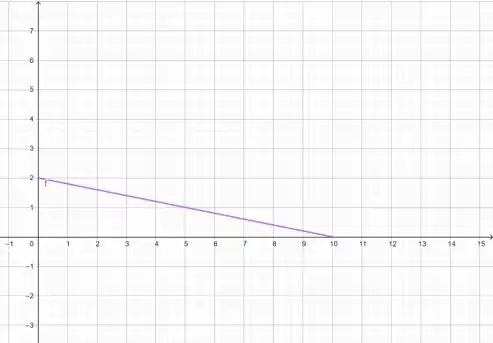
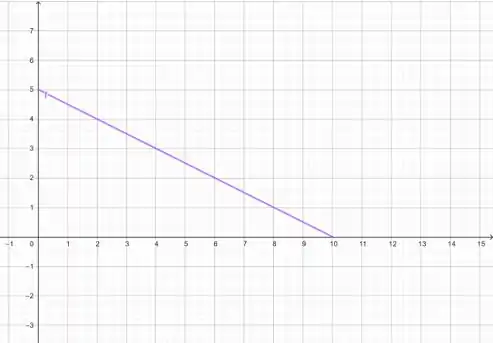
O corte com representa o valor inicial do item.