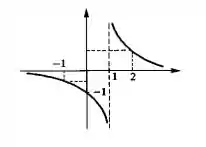
Esboce o gráfico da função dada implicitamente pela equação
Passo 1
Primeiro vamos deixar explicitamente em função de . Como? Isolando no lado esquerdo da equação :
E agora invertendo os dois lados da equação (e assim isolando ) temos:
Beleza até aqui?
Passo 2
Ok! Temos aqui a função e como já estamos carecas de saber, ela tem a cara de uma hipérbole deslocada. Se você não lembra, não tem problema! É só voltar alguns exercícios atrás e dar uma espiadinha no nosso conteúdo sobre as hipérboles, ta ok?
O comportamento dela vai ser o seguinte:
- Quando aumenta, o denominador também aumenta. Sendo assim, o valor de vai ficando cada vez menor, ou seja, ele tende a zero quando tende a infinito.
- Mas e quando se aproxima de por valores maiores do que ? Bom, daí o denominador vai ficando cada vez menor (positivo, mas pequeno). E se fizermos a divisão de um número por outro muito pequeno, o resultado vais er um número bem grande! Então temos que quando vai chegando perto de , o valor de vai aumentando cada vez mais. Isso significa que em o gráfico apresenta uma assíntota vertical.
- Já se o tender a por valores menores do que , vamos ter o mesmo comportamento, mas agora para menos infinito.
Passo 3
Bom, agora que já determinamos o comportamento dela, vamos ao esboço do gráfico?
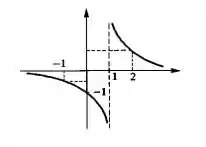
Resposta