Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 14.4 - Ex. 24

O índice de sensação térmica W é a temperatura que se sente quando a temperatura real for T e a velocidade do vento, v ; portanto, podemos escrever W = f T , v . A tabela de valores a seguir foi extraída da Tabela 1 da Seção 14.1.

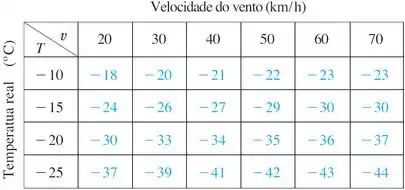
Use essa tabela para determinar a aproximação linear da função de sensação térmica quando T estiver a - 15 ° C e v estiver próximo de 50 k m / h . Estime, a seguir, a sensação térmica quando a temperatura estiver a - 17 ° C e a velocidade do vento for de 55 k m / h .

Passo 1

Show de bola, galera!

Vamos entender o que a questão nos pede!

A questão está pedindo para determinarmos a aproximação linear da função de sensação térmica W = f ( T , v ) quando a temperatura T está a - 15 ° C e a velocidade do vento v está próxima de 50 km/h, utilizando uma tabela de valores fornecida. Após determinar essa aproximação linear, o próximo passo é estimar a sensação térmica W quando a temperatura é de - 17 ° C e a velocidade do vento é de 55 km/h.

Como vamos resolver o primeiro passo?

  1. Estamos procurando uma aproximação para uma função de 2 variáveis, devemos nos lembrar que essa aproximação será dada por:

    2. f T , v ≈ f a , b + f T a , b T - a + f v a , b v - b

    Vamos fazer 2 estimas para f T ( a , b ) e f v ( a , b ) , respectivamente, e usar a média dessas estimativas como estimativa final. Ficou confuso?

    f T a , b ≅ f T , 1 a , b + f T , 2 a , b 2 f v a , b ≅ f v , 1 a , b + f v , 2 a , b 2

    E para estimar a sensação térmica

  2. temos que substituir o ponto dado no enunciado na função da sensação térmica encontrada no passo 1.

Passo 2

Precisamos encontrar f T - 15,50 e f v - 15,50 . Para colocarmos na equação da aproximação linear.

f T , v ≈ f a , b + f T a , b T - a + f v a , b v - b

Vamos começar com f T - 15,50 . Neste caso os valores da temperatura na tabela dada está variando de 5 em 5 . Com isso, temos que considerar a temperatura antes ( - 10 ) e depois ( - 20 ) .

f T , 1 - 1 0 , 50

f T - 15,50

f T , 2 - 20 , 50

Para encontrar f T , 1 , Substituindo na equação

f T , 1 a , b ≅ f T , 1 a , b + f T a , b 2

f T , 1 a , b ≅ f T , 1 - 10,50 + f T - 15,50 2

f T , 1 - 15,50 = f - 10,50 ⏞ - 22 - f - 15,50 ⏞ - 29 5 = 7 5

Para encontrar f T , 2 , Substituindo na equação

f T , 2 a , b ≅ f T , 2 - 2 0,50 + f T - 15,50 2

f T , 2 - 15,50 = f - 20,50 ⏞ - 35 - f - 15,50 ⏞ - 29 - 5 = 6 5

Passo 3

Vamos aplicar o mesmo procedimento para encontrar f v - 15,50 . Neste caso a os valores da velocidade na tabela dada está variando de 10 em 10 . Com isso, temos que considerar a velocidade antes ( 4 0 ) e depois ( 6 0 ) .

f v , 1 - 1 5 , 6 0

f v - 15,50

f v , 2 - 15 , 4 0

Para encontrar f v , 1 , Substituindo na equação

f v , 1 a , b ≅ f v , 1 a , b + f v a , b 2

f v , 1 a , b ≅ f v , 1 - 15,60 + f v - 15,50 2

f v , 1 - 15,50 = f - 15,60 ⏞ - 30 - f - 15,50 ⏞ - 29 10 = - 1 10

Para encontrar f v , 2 , Substituindo na equação

f v , 2 a , b ≅ f v , 1 - 15 , 4 0 + f v - 15,50 2

f v , 2 - 15,50 = f - 15,40 ⏞ - 27 - f - 15,50 ⏞ - 29 - 10 = - 2 10

Passo 4

Para obter f T - 15,50 , temos que fazer a média entre f T , 1 - 15,50 e f T , 2 - 15,50

f T - 15,50 ≅ f T , 1 - 15,50 + f T , 2 - 15,50 2

f T - 15,50 = 7 5 + 6 5 2

f T - 15,50 = 13 10

O mesmo para f v - 15,50 , temos que fazer a média

f v - 15,50 ≅ f v , 1 - 15,50 + f v , 2 - 15,50 2

f v - 15,50 = - 1 10 - 2 10 2

f v - 15,50 = - 3 20

Passo 5

Agora podemos aplicar a equação

f T , v ≈ f a , b + f T a , b T - a + f v a , b v - b

Em que:

a = - 15 b = 50

Substituindo

f T , v ≈ f - 15,50 + f T - 15,50 T + 15 + f v - 15,50 v - 50

Agora temos que substituir com o valores que encontramos

f - 15,50 = - 29

f T - 15,50 = 13 10

f v - 15,50 = - 3 20

Substituindo

f T , v ≈ - 29 + 13 10 T + 15 - 3 20 v - 50

Encontramos então a aproximação linear da sensação térmica.

Passo 6

Agora temos que estimar a sensação térmica quando a temperatura é de - 17 ° C e a velocidade do vento é de 55 km/h.

Utilizando a aproximação linear da sensação térmica

f T , v ≈ - 29 + 13 10 T + 15 - 3 20 v - 50

e substituindo T = - 17 e v = 55 , obtermos

f - 17,55 ≈ - 29 + 13 10 - 17 + 15 - 3 20 55 - 50

f - 17,55 ≈ - 29 + 13 10 - 2 - 3 20 5

Multiplicando os termos

f - 17,55 ≈ - 29 - 26 10 - 15 20

Fazendo MMC

f - 17,55 ≈ - 58 0 - 52 - 15 20

f - 17,55 ≈ - 647 20

f - 17,55 ≈ = - 32,35

Resposta

f T , v ≈ - 29 + 13 10 T + 15 - 3 20 v - 50

f - 17,55 ≈ - 32,35

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Nos Exercícios 33-38, encontre a linearização L(x, y) da função ƒ(x, y) em P0. Em seguida, encontre um limitante superior para a magnitude |E| do erro na aproximação ƒ(x, y) ≈ L(x, y) sobre o retângul
Nos Exercícios 25-30, encontre a linearização L(x, y) da função em cada ponto. f x , y = 3 x - 4 y + 5e m a ( 0,0 ) b ( 1 , 1 )
Encontre as linearizações L(x, y, z) das funções nos Exercícios 39-44 nos pontos determinados. f x , y , z = sin ⁡ x y z a( π 2 , 1 , 1 ) b )( 2 , 0 , 1 )
Nos Exercícios 45-48, encontre a linearização L(x, y, z) da função ƒ(x, y, z) em P0. Em seguida, encontre um limitante superior para a magnitude do erro E na aproximação ƒ(x, y, z) ≈ L(x, y, z) sobre
Nos Exercícios 33-38, encontre a linearização L(x, y) da função ƒ(x, y) em P0. Em seguida, encontre um limitante superior para a magnitude |E| do erro na aproximação ƒ(x, y) ≈ L(x, y) sobre o retângul