Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 8.4 - Ex. 22
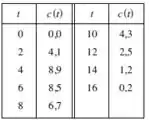
Depois de uma injeção de 5,5 mg de contraste, as leituras de concentração do contraste, em mg/L, a intervalos de dois segundos, são mostradas na tabela. Use a Regra de Simpson para estimar a capacidade cardíaca.
Passo 1
Essa questão é um pouco parecida com o exemplo 2 da seção do Stewart. Vamos resolvê-la!!
Usamos a Regra de Simpson para aproximar a integral da concentração, sabendo que , logo, . Lembrando que para essa regra:
Podemos substituir:
Então, pela fórmula que dá a frequência cardíaca
Resposta
Exercícios de Livros Relacionados
O valor exato da integral dada é π (confira). Aproxime a integral usando a a aproximação M 10 pelo ponto médio, b a aproximação trapezoidal T 10 e c a aproximação S 20 pela regra de Simpson usando a F
O valor exato da integral dada é π (confira). Aproxime a integral usando a a aproximação M 10 pelo ponto médio, b a aproximação trapezoidal T 10 e c a aproximação S 20 pela regra de Simpson usando a F
Encontre uma função g x da forma g x = A x 2 + B x + C Cujo gráfico contenha os pontos m - Δ x ,f m - Δ x ,m ,f m e m + x ,f m + Δ x , onde f x é a função dada, e para os valores dados de m e Δ x . En
Encontre uma função g x da forma g x = A x 2 + B x + C Cujo gráfico contenha os pontos m - Δ x ,f m - Δ x ,m ,f m e m + x ,f m + Δ x , onde f x é a função dada, e para os valores dados de m e Δ x . En
Use somas de Riemann para argumentar informalmente que integrar a velocidade escalar num intervalo de tempo produz a distância percorrida.