Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.Exercícios Práticos - Ex. 105

Integrações variadas

Calcule as integrais dos Exercícios 69- 116. As integrais estão listadas de maneira aleatória.

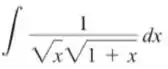
Passo 1

Para esta integral, por haver termos semelhantes na função, é possível resolvê-la por integração por substituição simples.

Passo 2

Com isso, pode-se fazer a substituição u = x ,   t a l   q u e   x = u ²   e   2 u d u = d x . Então:

∫ 1 x 1 + x d x = ∫ 2 u u 1 + u 2 d u = 2 ∫ 1 1 + u 2 d u

Passo 3

Nesta parte, deve-se perceber que a integral encontrada tem um valor pré-definido por uma propriedade que diz:

∫ d u u 2 + a 2 = ln ⁡ u + u 2 + a 2 + C ,   t a l   q u e   a = c t e .

Dessa forma, aplicando essa propriedade:

2 ∫ 1 1 + u 2 d u = 2 ln ⁡ u + u 2 + 1 2 + C

Passo 4

Após encontrar o resultado da integral, é necessário refazer as substituições a fim de retornar à variável x . Logo, fazendo u = x :

∫ 1 x 1 + x d x = 2 ln ⁡ x + x 2 + 1 + C

Como x 2 = x , então:

∫ 1 x 1 + x d x = 2 ln ⁡ x + x + 1 + C

Resposta

2 ln ⁡ x + x + 1 + C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

1.Calcule.C ) int x sqrt(1 + 3 x^2) d x
1.Calcule.int (1)/(( 3 x - 2 )^2)
2.Calcule:int_2^3 (1)/((x - 1)^3) d x
2.Calcule:int_1^2 (x)/(1 + 3 x^2) d x
2.Calculeint_(- (3)/(2))^(- 1) (2 x + 3)^(100) d x