Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.Exercícios Práticos - Ex. 107

Integrações variadas

Calcule as integrais dos Exercícios 69- 116. As integrais estão listadas de maneira aleatória.

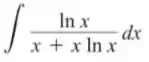
Passo 1

Para esta integral é possível resolvê-la por integração por substituição simples.

Deve-se lembrar, também, que a integral de uma soma é a soma das integrais.

E, para escolher a substituição a ser feita, pode-se rearranjar a função de outra maneira:

∫ ln ⁡ x x + x ln ⁡ x d x = ∫ ln ⁡ x x 1 + ln ⁡ x d x

Passo 2

Com isso, pode-se fazer a substituição u = 1 + ln ⁡ x , ln ⁡ x = u - 1 ,   t a l   q u e   d u = 1 x d x .

Então:

∫ ln ⁡ x x 1 + ln ⁡ x d x = ∫ ln ⁡ x 1 + ln ⁡ x d x x

∫ u - 1 u d u = ∫ d u - ∫ 1 u d u

Passo 3

Resolvendo essa integral, tem-se:

∫ d u - ∫ 1 u d u = u - ln ⁡ u + C

Passo 4

Para encontrar o resultado desejado, é necessário refazer a substituição a fim de voltar a variável x . Fazendo isso:

u - ln ⁡ u + C = ( 1 + ln ⁡ x ) - ln ⁡ 1 + ln ⁡ x + C

Como C + 1 resulta em outra constante, é possível simplesmente substituí-los por outra constante arbitrária, tal que:

( 1 + ln ⁡ x ) - ln ⁡ 1 + ln ⁡ x + C = ln ⁡ x - ln ⁡ 1 + ln ⁡ x + K

Resposta

ln ⁡ x - ln ⁡ 1 + ln ⁡ x + K

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

1.Calcule.A) ∫ tan 3 ⁡ x sec 4 ⁡ xd x
Calcule. ∫ 2 x - 3 d x
Calcule. ∫ ( 5 x - 1 + 2 x ) d x
Calcule. ∫ 1 2 x + 3 d x
Calcule a integral ∫ sec ⁡ y tg ⁡ yd y 2 + sec ⁡ y