Enunciado
Cálculo - Cálculo - 12ª Edição - Maurice D. Weir e Joel Hass (George B. Thomas)- Ed: 12º - Capítulo 8.7 - Ex. 77 a
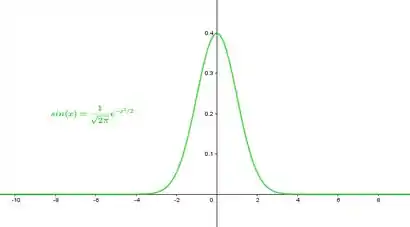
A integral
é chamada função densidade de probabilidade normal, com média e desvio padrão e tem aplicações importantes em probabilidade e estatística .
- Trace o gráfico do integrando . Determine os intervalos em que f é crescente, decrescente e quaisquer valores extremos locais e onde eles ocorrem.
Passo 1
Inicialmente considere em seguida identificaremos se possui pontos críticos para isso faremos, ou seja,
Igualando a zero,
Como a exponencial nunca se anula
Isso significa que é um número crítico.
Vamos analisar o que acontece com a função nas proximidades dele.
Perceba que, para valores dentro do intervalo , assume valores positivos (cresce). E para valores dentro do intervalo , irá assumir valores negativos (decresce). Logo, é um ponto de máximo no intervalo de
Passo 2
Determinaremos agora .
Como já determinamos podemos verificar se ela possui pontos inflexão, para isso faremos , ou seja,
Perceba que, para valores dentro do intervalo , assume valores positivos (tem concavidade para cima). E para valores dentro do intervalo , irá assumir valores negativos ( tem concavidade para baixo). Logo, é um ponto de inflexão no intervalo de ou seja, possui uma mudança de concavidade nesse ponto.
Já, para valores dentro do intervalo irá assumir valores positivos ( tem concavidade para cima). E para valores dentro do intervalo 0 , irá assumir valores positivos ( tem concavidade para cima). Logo, não é um ponto de inflexão no intervalo de
Passo 3
Perceba que não tem assíntota vertical, pois nunca se anula.
Porém ,
Resposta
