A integral representa o volume de um sólido. Descreva o sólido.
Passo 1
Integrando com respeito a indica que tivemos uma rotação em torno do eixo , onde nosso raio interno é dado por e o raio externo é 3. Ou seja, nosso sólido é obtido girando a região no intervalo em torno do eixo . A figura que vai ser rotacionada em torno do eixo pode ser vista na seguinte imagem
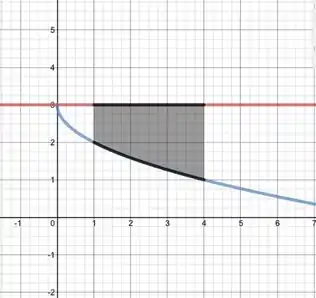
Resposta
Ei, a resposta está no passo a passo :)