Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.3 - Ex. 62
No intervalo de temperatura entre e , a resistência [em ohms] de um certo termômetro de resistência de platina é dada por:
onde é a temperatura variando entre e . Quando, no intervalo de variação da temperatura, a resistência é mais e menos sensível à variação de ? [Sugestão: Considere o tamanho de no intervalo .]
Passo 1
Bom, nós precisamos encontrar onde a resistência tem valor máximo e mínimo, para saber onde a resistência é menos e mais sensível à variação de temperatura. E, se liga, em qualquer gráfico, tanto no ponto de máximo quanto o de mínimo a derivada da função é zero! Isso porque nesses pontos a reta tangente é horizontal!
E olhando para a nossa expressão de , vemos que ela é uma parábola (é uma equação do segundo grau) com a concavidade voltada para baixo (porque o fator que multiplica o termo ao quadrado é negativo), logo só teremos um valor para a derivada ser zero e esse será o ponto máximo.
Passo 2
Calculando esse valor máximo, nele a derivada da função é zero, então:
Logo:
Então, em , nós temos a menor sensibilidade da resistência à temperatura.
Passo 3
Agora, pensa comigo, se nós temos uma parábola desse tipo:
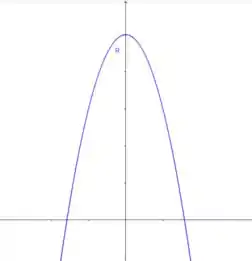
Você concorda comigo que os pontos mínimos são nos extremos direito e esquerdo do gráfico? Então, no nosso intervalo de a , é justamente em e em onde a resistência possui seu valor mínimo, o que caracteriza maior sensibilidade à temperatura.
Resposta
Menor sensibilidade em e maior sensibilidade em e em .