Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.1 - Ex. 48
Investigue a família de curvas definidas pelas equações paramétricas
Passo 1
A questão pede para estudarmos o comportamento da curva parametrizada
Assim, faremos vários plots para diferentes valores de :
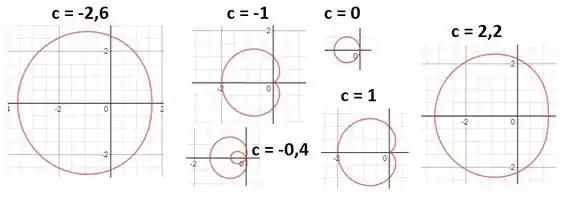
Vemos que conforme vai se tornando grande, a curva vai se aproximando de uma circunferência. Já para pequeno em módulo (entre e ) o formato muda bastante!
Resposta
Esboço de gráfico.
Exercícios de Livros Relacionados
Se um projétil for atirado com uma velocidade inicial v 0 metros por segundo com um ngulo α acima da horizontal e a resistência do ar for considerada desprezível, então sua posição, depois de t segund
Investigue, com o auxílio de uma ferramenta gráfica, a família de curvas definidas pelas equações paramétricas x = cos t y = sen t - sen c t c0 Comece tomando c como um inteiro positivo e veja o
Investigue a família de curvas definidas pelas equações paramétricas x = t 2 y = t 3 - c t Como muda o formato quando c aumenta? Ilustre traçando vários membros da família com o auxílio de uma ferrame
As curvas com equações x = a sen n t y = b cos t São chamadas de figuras de Lissajous. Investigue, com o auxílio de uma ferramenta gráfica, como essas curvas mudam quando a , b e n variam. (Tome n
Elimine o parâmetro para encontrar uma equação cartesiana da curva: x = t y = 1 - t