Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 11.12 - Ex. 9
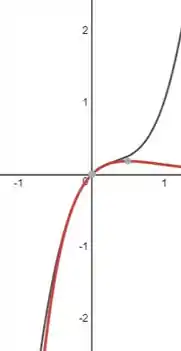
Encontre o polinômio de Taylor da função em . Trace e na mesma tela.
Passo 1
Faaala, pessoal, tudo certo??
Essa questão pede pra gente achar o polinômio de Taylor de uma função...
Pra encontrar o , vamos primeiro encontrar a série de Taylor de centrada em , e depois expandir até o grau .
Já adianto que a gente vai precisar lembrar a série exponencial:
Por último, vamos traçar a função e o em uma mesma tela usando um software.
Passo 2
Primeira coisa que vamos perceber é que dentro da nossa função, temos uma exponencial! Então por isso a gente vai poder substituir essa parte pela série exponencial. Só que o termo que aparece não é , mas sim , então no lugar do , vai aparecer um :
Então temos que
Esse que está multiplicando a gente pode incorporar na nossa série, e fica assim:
Passo 3
Para calcularmos , vamos abrir o somatório:
Como queremos só até o grau :
Passo 4
Pra terminar, vamos traçar a função e no plano:
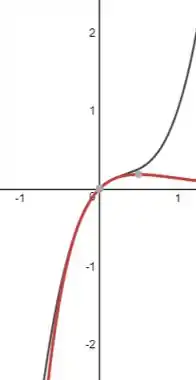
De vermelho temos a função e em cinza .
Resposta
