Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 77
- Investigue a família de curvas definidas pelas equações polares , onde é um inteiro positivo. Como o número de laços está relacionado a ?
- O que aconteceria se a equação na parte (a) fosse trocada por ?
Passo 1
O enunciado da questão nos dá uma noção de que o gráfico de vai ter alguns laços e nos pede pra investigar esses laços no item a.
Para isso, a gente vai substituir por alguns valores inteiros e analisar os gráficos.
E no item b vamos analisar esses gráficos com o valor do seno em módulo.
Para analisar esses gráficos, vamos criá-los em uma ferramenta gráfica.
Passo 2
- Para iniciar a análise, vamos olhar gráficos para alguns valores de :
- Vamos novamente dar uma olhada nos gráficos para alguns valores de
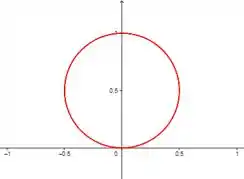
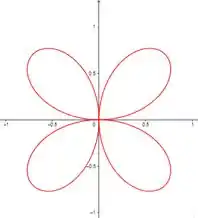
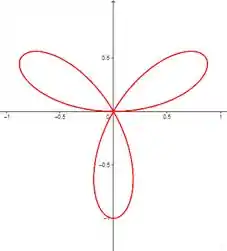
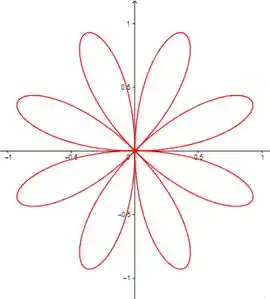
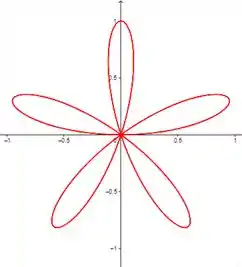
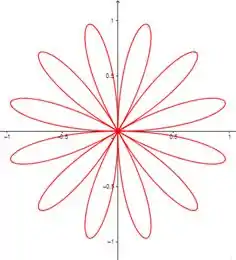
Percebeu algum padrão?? Chega mais 😉
Passo 3
Para ímpar o número de laços é igual a , podemos ver isso nos gráficos com igual a e .
Já para par o número de laços é o dobro de , como podemos ver com igual a e .
Escrevendo de uma forma mais elegante, se chamarmos o número de laços de teremos que
, para
, para
Passo 4
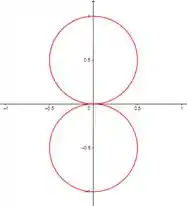
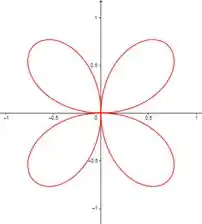
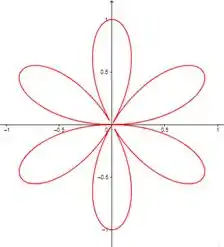
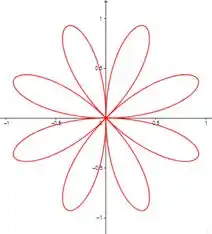
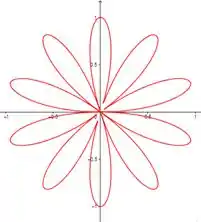
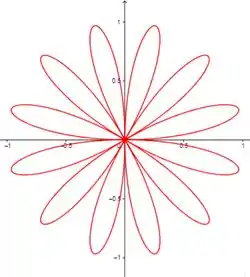
Comparando os gráfico de com , para números pares de não temos diferenças, mas para números impares temos sim.
Quando colocamos o módulo na equação, para todos os valores de temos que o número de laços é o dobro de .
Resposta
a) Seja o número de laços, então:
, para
, para
b) Comparando os gráfico de com , para números pares de não temos diferenças, mas para números impares temos sim.