Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 3.11 - Ex. 58
Investigue a família das funções
onde é um inteiro positivo. Descreva o que acontece com o gráfico de quando se torna maior.
Passo 1
Fala galera, nessa questão temos a seguinte função:
Que na verdade é uma família de funções, se você trocar o você obtêm uma função, e assim, você tem várias funções para vários .
Nessa questão vamos plotar o gráfico de uma função dessa família de funções para um determinado e depois vamos aumentando o valor de e plotando novos gráficos, no final, devemos indicar o que foi que ocorreu de diferente entre um gráfico e outro para vermos o que acontece com o gráfico quando aumenta.
Passo 2
Vamos dar uma olha no gráfico...
Pra :
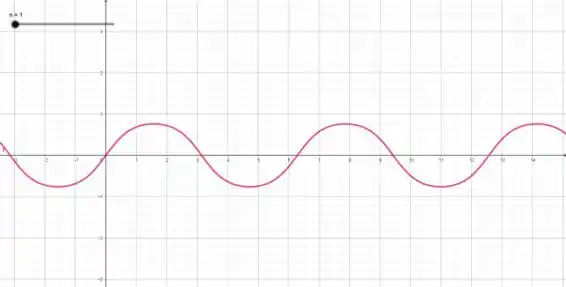
Quando aumentamos o valor de , a função vai perdendo essa forma “arredondada”...
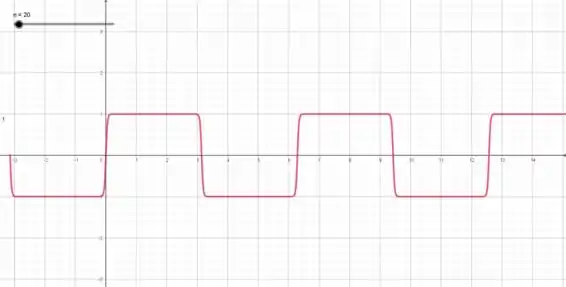
E ela se mostra quase constante nesse formato quando aumentamos mais o valor de
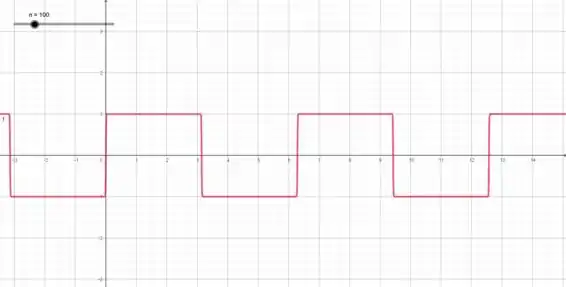
Passo 3
Ou seja, o gráfico vai sendo formado por “retas” verticais e horizontais, a medida que aumentamos o valor de . O gráfico vai ficando “quadradinho”.
Isso é, ele vira um reta horizontal (um valor constante) para subintervalos.
Resposta
Se tornou constate por subintervalos.