Enunciado
Cálculo - Cálculo com Geometria Analítica Volume 1 - 3ª Edição - Louis Leithold- Ed: 3º - Capítulo 8.Revisão - Ex. 18
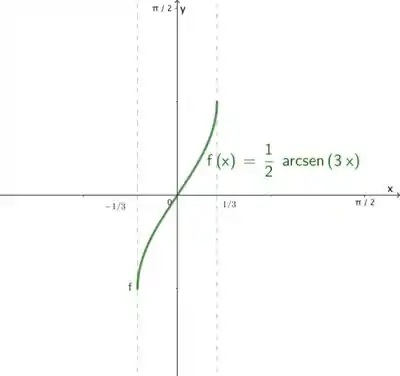
Faça um esboço do gráfico da função
Passo 1
Pessoal, para esboçar o gráfico desta função, nós precisamos ter uma ideia de como é o gráfico da função , e a partir dele nós vamos usar transformações até chegar no gráfico da função pedida.
Devemos lembrar que é a função inversa do e que seu domínio é com imagem sendo o intervalo Segue o gráfico de .
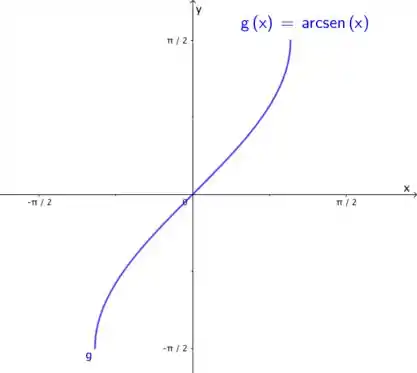
Passo 2
A primeira transformação que faremos no gráfico elementar para se tornar o gráfico da é multiplicar por e ficar com . O que isso vai mudar no meu gráfico inicial?
Bom, quando multiplicamos o por uma constante , a interpretação geométrica é que o gráfico vai ser comprimido horizontalmente. Assim, o domínio vai mudar, pois, neste caso, devemos ter , e dividindo tudo por , temos
.
O gráfico será
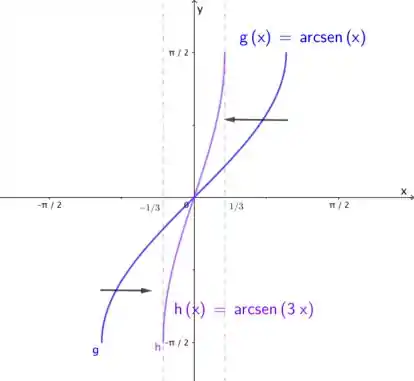
O domínio é com imagem sendo o intervalo
Passo 3
Agora devemos perceber que é dividida por , isso indica que todos os valores de em serão divididos por dois, o que vai fazer o gráfico de ser comprimido verticalmente e alterar a sua imagem.
Sabemos que , então multiplicando tudo por , temos
Sendo assim, a imagem de é e o domínio continua
O gráfico vai ser
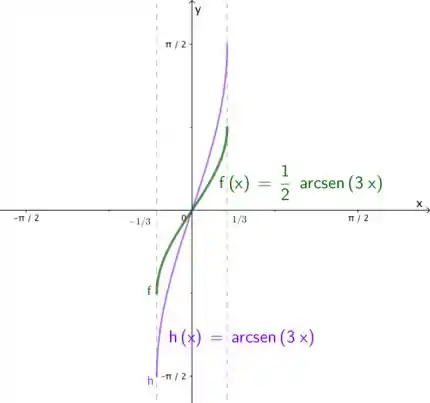
Resposta
