Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 4.6 - Ex. 40
- Investigue a família de funções polinomiais dada pela equação . Para quais valores de a curva tem pontos de mínimo?
- Mostre que os pontos de máximo e de mínimo para cada curva da família estão sobre a curva . Ilustre fazendo o gráfico dessa parábola e de vários membros da família.
Passo 1
- Digamos que é um número crítico para . Então, . Assim,
Assim, tem pontos críticos em
Para , em , então não muda o sinal até , e não há valor extremo.
Se , então muda de positivo para negativo em e de negativo para positivo em . Assim, tem um máximo em e um mínimo local em .
Passo 2
Então, o ponto é ; isto é, o ponto fica na curva .
Esboço do gráfico:
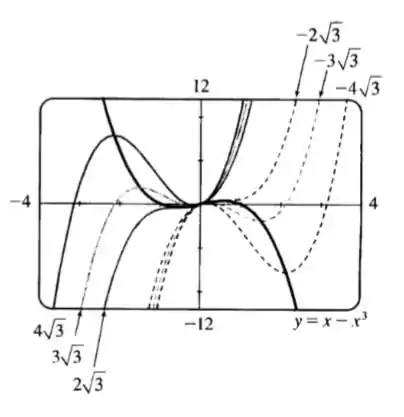
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Use o roteiro dessa seção para esboçar a curva. y = 2 x 5 - 5 x 2 + 1
Esboce o gráfico de uma função que satisfaça todas as condições dadas. f ' x0 para todo x ≠ 1 , assíntota vertical x = 1 , f ' ' x0 se x1 ou x3 , f ' ' x0 se 1x3
Esboce o gráfico de uma função que satisfaça todas as condições dadas. f ' 0 = f ' 2 = f ' 4 = 0 , f ' x0 se x0 ou 2x4 , f ' x0 se 0x2 ou x4 , f ' ' x0 se 1x3 , f ' ' x0 se x1 ou x3
Esboce o gráfico de uma função que satisfaça todas as condições dadas. f ' 1 = f ' - 1 = 0 , f ' x0 se x1 , f ' x0 se 1x2 , f ' x = - 1 se x2 , f ' ' x0 se - 2x0 E ponto de inflexão em 0,1
Esboce o gráfico de uma função que satisfaça todas as condições dadas. f ' x0 se x2 , f ' x0 se x2 , f ' - 2 = 0 , lim x → 2 f ' x = ∞ , f ' ' x0 se x ≠ 2