Enunciado
Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 7.4 - Ex. 16
Calcule a integral.
Passo 1
Bem, para achar o valor dessa integral vamos calcular a integral indefinida dela e depois utilizamos o Teorema Fundamental do Cálculo para aplicar os limites de integração.
Como o grau do numerador é maior que o grau do denominador, vamos dividir os dois:
Dividindo por vamos ter um quociente e resto , assim:
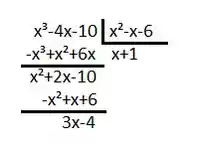
Agora vamos fatorar o denominador, achando as raízes de temos:
Usando Bhaskara:
Temos então:
Assim ficamos com:
Passo 2
Temos o Caso I, onde o denominador é um produto de fatores lineares sem repetição:
Vamos achar os valores de e , vamos multiplicar os lados da equação pelo produto dos denominadores :
Vamos destrinchar agora e isolar os termos do polinômio:
Temos uma igualdade de polinômios, então valos igualar os coeficientes de de cada lado, e os termos constantes também, assim vamos ficar com o sistema:
Isolando na primeira e substituindo na segunda, ficamos com:
Assim achamos :
Pronto, achamos os valores de e , vamos agora substituir de volta na integral:
Pronto, agora vamos resolver as quatro separadamente.
Passo 3
A primeira é fácil achar as primitivas da função, usando uma expressão da Tabela de Integrais Indefinidas:
Agora é só aplicar:
A segunda também é simples achar as primitivas da função, usando uma expressão da Tabela de Integrais Indefinidas:
Agora é só aplicar:
Passo 4
Com a terceira vamos usar a Regra da Substituição, vamos fazer uma mudança de variável para encontrar o valor dessa integral, vemos que temos um no denominador, podemos então usar a mudança de variável:
Vamos agora achar diferencial de , derivando:
Fazendo a substituição ficamos com:
Agora é fácil achar as primitivas da função, usando uma expressão da Tabela de Integrais Indefinidas:
Agora é só aplicar:
Passo 5
Com a quarta vamos usar a Regra da Substituição, vamos fazer uma mudança de variável para encontrar o valor dessa integral, vemos que temos um no denominador, podemos então usar a mudança de variável:
Vamos agora achar diferencial de , derivando:
Fazendo a substituição ficamos com:
Agora é fácil achar as primitivas da função, usando duas expressões da Tabela de Integrais Indefinidas:
Agora é só aplicar:
Passo 6
Juntando temos:
Calma, não terminou ainda, não esqueça de voltar para a variável , é só substituir de volta o que você usou no começo:
Pronto, já encontramos a integral indefinida. Perceba que nem seria necessário colocar a constante de integração nesse caso, pois a gente usou a integral indefinida mais como uma ferramenta para calcular a integral. Agora é só calcular a integral definida usando o Teorema Fundamental do Cálculo:
Vamos lá: