Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 1 - 6ª Edição - James Stewart- Ed: 6º - Capítulo 5.2 - Ex. 50

Encontre int_0^5 f (x) d x se

f (x) = {[[3 , p a r a x < 3],[x , p a r a x >= 3]])

Passo 1

E aí, galerinha!

Nesse problema queremos calcular a integral da função f (x) entre x = 0 e x = 5 sendo que

f (x) = {[[3 , p a r a x < 3],[x , p a r a x >= 3]])

Tem ideia de como fazemos isso?

Como no intervalo de integração a função não está definida continuamente, devemos separar as integrais, sendo uma para cada definição da função f :

int_0^5 f (x) d x = int_0^3 f (x) d x + int_3^5 f (x) d x

int_0^5 f (x) d x = int_0^3 (3) d x + int_3^5 (x) d x

Veja só!

Passo 2

Procuramos então a área de um retângulo mais um triangulo isósceles, de forma que temos a figura:

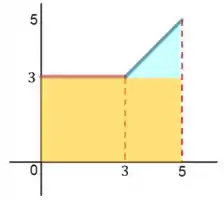
Logo, as integrais são a área da figura:

int_0^5 f (x) d x = A r e a a m a r e l a + A r e a a z u l

int_0^5 f (x) d x = 3 (5) + (1)/(2) (2) (2)

int_0^5 f (x) d x = 17

E aí! o que achou? Responde Aí!

Resposta

int_0^5 f (x) d x = 17

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Seja f 0 = 0 e f x = 1 x se 0x ≤ 1 . Mostre que f não é integrável em 0,1 . [Sugestão: mostre que o primeiro termo na soma de Riemann, f x i * Δ x , pode ser tornado arbitrariamente grande.]
Use as propriedades das integrais, junto com os exercícios 27 e 28 , para demonstrar a desigualdade. ∫ 1 3 x 4 + 1d x ≥ 26 3
Use a Propriedade 8 para estimar o valor da integral. ∫ π 4 π 3 tg ⁡ xd x
Use a Propriedade 8 para estimar o valor da integral. ∫ 0 2 x e - xd x
Use a Propriedade 8 para estimar o valor da integral. ∫ 0 2 x 3 - 3 x + 3d x