Enunciado
Cálculo - James Stewart - Vol 1- Ed: 8º - Capítulo 4.3 - Ex. 7
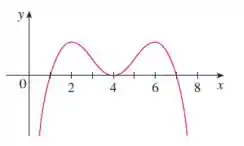
Em cada item, indique as coordenadas x dos pontos de inflexão de f. Dê razões para suas escolhas.
(a) Esta curva é o gráfico de f.
(b) Esta curva é o gráfico de .
(c) Esta curva é o gráfico de .
Passo 1
Algumas vezes na nossa vida chegamos a um ponto que sentimos que temos que mudar algo, né não? Na matemática também acontece. Assim é o ponto de inflexão, onde a concavidade se revolta e muda de direção hehe.
Analisando o gráfico de f,
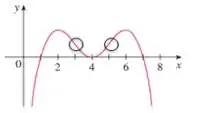
O ponto de inflexão é em x=3 pois a concavidade muda de baixo para cima. E também em x=5, onde a concavidade muda de cima para baixo.
Passo 2
Para o gráfico de , usamos o teste da Primeira Derivada. Precisamos encontrar os pontos máximos e mínimos. Para um valor de máximo temos x=2 e x=6 e é onde , muda de positivo para negativo.
Em x=4, é um mínimo, onde , muda de negativo para positivo.
Passo 3
Para o gráfico de , usamos o teste da Segunda Derivada. Esse teste nos diz que e então f tem um mínimo local. Esse ponto é em x=1, porque muda de negativo para positivo lá e, portanto, o gráfico muda de côncavo para baixo para côncavo para cima.
Para e então f tem um máximo local. Esse ponto é em x=7, porque muda de positivo para negativo lá, e assim o gráfico muda de côncavo para cima e côncavo para baixo.
Resposta
(a) x=3, pois a concavidade muda de baixo para cima. E também em x=5, onde a concavidade muda de cima para baixo.
(b) Para um valor de máximo temos x=2 e x=6 e em x=4, é um mínimo.
(c) Em x=1 e em x=7.