Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.3 - Ex. 5
Esboce a região cuja área é dada pela integral e calcule-a.
Passo 1
Falaaaa aí pessoal, vamos lá resolver essa questão?! Simbora então!
Então, a questão pede para fazer um esboço da região de integração e determinar o valor da integral.
Como vamos fazer isso?
Observe que a integral está em coordenadas polares. E olhando os valores de integração, veja que temos o raio variando de a e o ângulo variando de a . Logo podemos concluir que se trata de uma região que está entre dois círculos, e delimitada pelos ângulos dados.
Para resolver a integral, começamos pela integral de dentro em , aplicamos os limites de integração. Na sequência integramos em e novamente aplicamos os limites de integração.
Bora lá resolver!!!
Passo 2
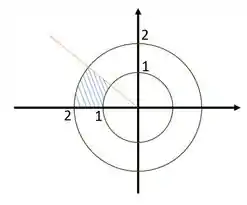
Bom vamos começar fazendo um esboço da região.
Observe o gráfico a baixo, e vê se concorda com o que mencionamos antes:
Agora, analisa comigo os intervalos de integração.
O raio está variando de a , ou seja, ele forma uma espécie de anel. Pois temos dois círculos.
Mas a gente não quer todo esse anel, queremos apenas a parte preenchida ali, e isso se dá pela variação de , que varia de a .
Perceba que essa variação de acontece no sentido horário, ou seja, descresce.
Passo 3
Beleza, fizemos o bendito esboço do grafico. Agora vamos lá resolver a integral!
Vamos resolver como estamos acostumados. Começando de dentro para fora.
A integral de dentro, ou seja, em :
Integrando:
Aplicando os limites de integração, temo:
Agora vamos ficar com uma integral simples em .
Integrando novamente, vamos ter:
Aplicando os limites de integração,
Logo, vamos ter como resposta:
Passo 4
Encontramos nossa área como:
Beleza, mas observe, estamos calculando a área da nossa região, tem área negativa?!
Não tem como né, então vamos pegar a parte positiva desse resultado, ou seja:
Porque isso aconteceu? O resultado ficou negativo, porque a integral está avaliando no sentido horário. Integrando de até . Simplesmente por isso.
Resposta
