Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.7 - Ex. 28
Uma janela normanda tem a forma de um retângulo tendo em cima um semicírculo. (O diâmetro do semicírculo é igual à largura do retângulo). Se o perímetro da janela for , encontre as dimensões da janela que deixam passar a maior quantidade possível de luz.
Passo 1
E aí! como vai?
Nesse problema temos uma janela que é formada por um retângulo e um semicírculo cujo diâmetro é igual à largura do retângulo.
A partir daí queremos descobrir qual é a maior area possivel para essa janela para um perímetro total de .
Tem ideia de como fazemos isso?
Aqui temos um problema de otimização e temos que otimizar a área de um objeto (no caso a janela) a partir do seu perímetro que é fixo.
Para resolver esse tipo de problema, temos que desenvolver a equação que é fixa (no caso o perímetro) e substituir na equação que queremos otimizar (no caso a area da janela).
Com as informações do enunciado a gente faz a seguinte figura:
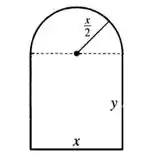
Para otimizar a função area dessa janela vamos usar a ideia de máximos e mínimos... ou seja, vamos derivar a area em função de alguma variável e igualar a .
A partir daí, vamos substituir na equação da area e analisar os resultados.
Sacou? Bora começar!
Passo 2
Vamos começar determinando a equação do perímetro dessa janela.
Com base no esboço do passo podemos determinar que
Onde é a metade da circunferência de raio .
Foi dito que o perímetro é fixo em .
Agora vamos determinar a equação da área da janela.
Tranquilo até aqui?
Passo 3
Para maximizar a função área temos que deixá-la em função de uma única variavel...
Então aqui entra a jogada de mestre... vamos isolar uma dessas variáveis na equação do perímetro e substituir em . assim vamos ficar com uma função de uma única variavel.
Substituindo em
Agora que temos em função de uma única variavel vamos derivá-la e igualar a .
Então o valor de que maximiza a função é .
Substituindo na equação do perímetro podemos determinar tambem o valor de
Então as dimensões da janela é de largura e de altura.
E aí! o que achou? Responde Aí!
Resposta
de largura e de altura.