Uma janela de observação em um submarino é um quadrado com de lado. Usando como o peso específico da água do mar, encontre a força exercida pelo fluido sobre a janela
quando o submarino estiver submerso de tal forma que a janela esteja vertical e seu topo se encontre a uma profundidade de pés.
Passo 1
De inicio nós temos a primeira informação: é uma janela quadrada com ! A segunda info é o submarino de estar submerso de tal forma que a janela esteja vertical e seu topo se encontre a uma profundidade de pés. Certo, né? Vamos começar!!
Para facilitar a nossa compreensão, temos o diagrama:
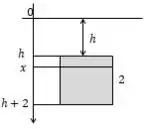
Passo 2
A partir da figura, podemos começar integrando:
Daí é só resolvermos a integração!
Resolvendo o produto notável, temos:
Portanto, a força exercida pelo fuido, na consição dada pelo enunciado é:
Prontinho!!