Enunciado
Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 6.11 - Ex. 2d
Sem calcular a integral, verificar as seguintes desigualdade:
Passo 1
Quando se trata de funções trignometricas é SEMPREEEE bom ter o gráfico de todas elas em mente, pois isso pode ajudar muito na resolução de uma questão e é justamente pode meio desse método que vamos resolver a questão.
Além disso vamos utilizar a seguinte propriedade
Passo 2
Agora vamos dar uma relembrada no gráfico da função cosseno...
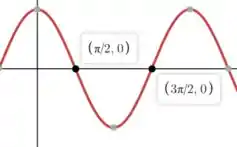
Vemos que essa função no nosso intervalo de interesse é negativa. Dessa forma, o valor da integral também será o que implica em nossa afirmação ser verdadeira.
Resposta
Verdadeira
Exercícios de Livros Relacionados
Calcule a integral:42) ∫ 1 2 1 2 4 1 - x ² . d x ²
Calcule a integral:24) ∫ 1 8 x 3 . d x
Calcule a integral:34) ∫ 0 3 ( 2 s e nx - e x ) . d x
Calcule a integral:29) ∫ 1 9 x - 1 x . d x
Calcule a integral:37) ∫ 0 1 ( x e + e x ) . d x