Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Diva Flemming - Cálculo A- Ed: 6º - Capítulo 6.11 - Ex. 5b

Verificar se o resultado das seguintes integrais é postivo, negativo ou zero, sem calculá-las

∫ 0 2 π s e n t d t

Passo 1

Quando se trata de funções trignometricas é SEMPREEEE bom ter o gráfico de todas elas em mente, pois isso pode ajudar muito na resolução de uma questão e é justamente pode meio desse método que vamos resolver a questão.

Como se trata da função seno, vamos relembrar seu gráfico.

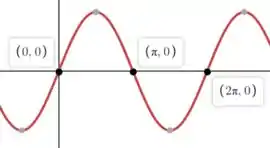
Para resolver essa questão vamos precisar de outra propriedade a respeito de integrais

Se a f é integrável em [a,c] e em [c,b], então f é integrável em [a,b] e

∫ a b f x = ∫ a c f ( x ) +   ∫ c b f ( x )

Passo 2

Vamos usar as ferramentas acima na resolução de nossa questão.

∫ 0 2 π s e n t d t =   ∫ 0 π s e n t d t +   ∫ π 2 π s e n t d t

Analisando cada termo do lado direito separadamente com o auxilio do gráfico, vemos que se :

∫ 0 π s e n t d t = I

Entao

∫ π 2 π s e n t d t =   - I

Passo 3

Somando as duas equações temos que:

∫ 0 2 π s e n t d t =   I +   - I = 0

Portanto,seu valor é nulo.

Resposta

Nulo

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Use a Parte 1 do Teorema Fundamental do Cálculo para encontrar a derivada da função.18) y = ∫ s e nx 1 1 + t ² . d t ²
Use a Parte 1 do Teorema Fundamental do Cálculo para encontrar a derivada da função. y = ∫ 1 x 4 θd θ
Use a Parte 1 do Teorema Fundamental do Cálculo para encontrar a derivada da função. h ( x ) = ∫ 1 x z 2 z 4 + 1 d z
Calcule a integral:23) ∫ 0 1 x 4 5 d x
Calcule a integral:36) int_1^(18) sqrt((3)/(z)) . d z