Kelly parte de Winnipeg às 14h e dirige a uma velocidade constante para oeste na rodovia Trans-Canadá. Ela passa por Brandon, a 210km de Winnipeg, às 16h.
- Expresse a distância percorrida em função do tempo decorrido.
- Desenhe o gráfico da equação da parte (a).
- Qual é a inclinação desta reta? O que ela representa?
Passo 1
Fala aí, pessoal! 😎

Nesse problema temos uma pessoa que percorre um trajeto entre dois locais com velocidade constante em que em um local ela passou às e em outro local, a de distância passou às .
A partir daí queremos expressar a distância percorrida em função do tempo decorrido, desenhar o gráfico da equação da parte (a) e obter qual é a inclinação desta reta e o que ela representa.
Parece complicado? 😐
Confia que você vai ver que não é. Para encontrarmos a distância em função do tempo, devemos lembrar dos nossos conhecimentos de física, onde a velocidade, a distância e o tempo se relacionam da seguinte forma:
velocidade
deslocamento
tempo decorrido
Com a velocidade em mãos, sendo ela constante, poderemos relacionar os deslocamentos seguintes com o tempo passado.
Passo 2
Letra (a)
Vamos utilizar a equação
O indica variação, então o que temos é e , mas o que vamos fazer é considerar Winnipeg como espaço inicial, então
Já o tempo inicial em Winnipeg é o dado no enunciado:
Já em Brandon, temos o deslocamento dado de:
Agora o tempo em Brandon é o que nos foi dado no enunciado:
Sendo assim, nos resta agora substituir os valores que encontramos:
Com isso em mãos, poderemos pensar agora em um caso genérico, onde temos um deslocamento realizado em um intervalo de tempo , com essa mesma velocidade. Utilizando ainda da relação:
Passo 3
Letra (b)
O gráfico a gente vai fazer utilizando o GeoGebra, mas irei lhe explicar o comportamento dele. Veja que a função que encontramos,
Tem a estrutura de uma reta,
Onde o termo
Sendo assim, ela corta o eixo em , já por ter , ela é uma reta crescente. Dito isso, vamos gerar o gráfico:
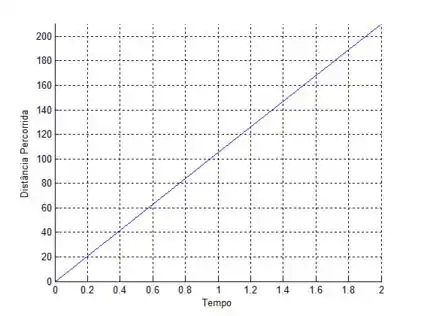
Bacana, não é? 😇
Passo 4
Letra (c)
Analisando novamente a equação genérica de uma reta, temos:
Onde é chamado coeficiente angular da reta. E é ele que dita a inclinação da reta, e se a função será crescente ou decrecente, mais para frente nos seus estudos de cálculo você vai aprender mais algumas informações sobre esse coeficiente e até outras formas de encontrá-lo.
Mas agora, se analisarmos a equação padrão e a que encontramos, vemos que a inclinação da reta é , e representa a velocidade constante do carro de Kelly. Algo que encontramos na letra a).
E aí! entendeu tudo? Responde Aí! 😁

Resposta
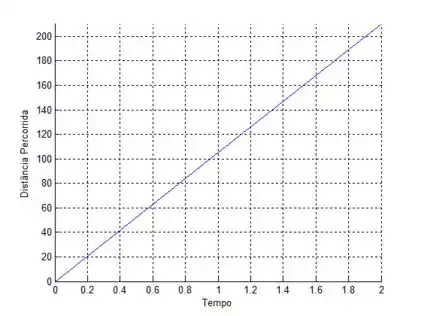
- A inclinação da reta é , e representa a velocidade constante do carro de Kelly.