Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 1.2 - Ex. 7
O que todos os membros da família de funções lineares têm em comum? Esboce os gráficos de vários membros da família.
Passo 1
Fala, galera! Beleza? Vamos resolver essa questão!
O enunciado pediu pra gente determinar o que todos os membros da família de funções lineares têm em comum e esboçar os gráficos de vários membros dessa família.
Pra isso, temos que notar que é uma constante que pode assumir qualquer valor real. Então poderíamos ter:
E por aí vai! Então, podemos ter infinitas funções. Mas o que todas elas vão ter em comum?
Bom, quando dizemos que é uma função linear de , queremos dizer que o gráfico da função é uma reta. Assim, podemos dizer uma fórmula para a função na forma:
Onde é o coeficiente angular ou inclinação da reta e é o coeficiente linear ou interseção com o eixo . Então, como temos uma função linear, o que nós vamos fazer é comparar os elementos da nossa família de funções com a equação da reta e o que eles significam para verificar o que cada membro da família tem em comum.
Vamos lá!
Passo 2
Escrevendo a nossa função no formato da equação da reta, temos:
Observe que nesse caso, temos e . Isso significa que mudando o valor de , estaremos mudando o ponto onde a reta intercepta o eixo . Mas observe que, mesmo mudando o valor de , teremos sempre a inclinação .
Daí a gente já percebe uma coisa, que as retas terão em comum, todas tem o coeficiente angular igual a . Isso significa que são retas decrescentes, porque a inclinação é negativa.
Além disso como apenas o coeficiente linear varia, isso significa que todas as retas dessa família serão paralelas entre si!
Tranquilo até aqui? 😊
Passo 3
Para fazer o gráfico vamos escolher os valores . Assim, teremos as seguintes funções:
Então, considerando as características dessa família, que nós vimos no passo anterior, e plotando os gráficos com a inclinação e os pontos de intercepção dados por , teremos:
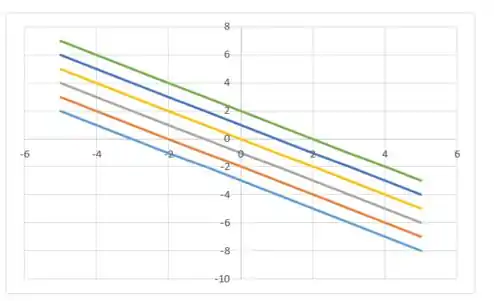
Valeu, galera! Até a próxima! 😉