Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 15.4 - Ex. 22

Uma lâmina com densidade constante ρ x ,   y = ρ ocupa a região dada. Encontre os momentos de inércia I x e I y e os raios de giração x - - e y - - do triângulo com vértices 0 ,   0 ,   b ,   0 ,   ( 0 ,   h )

Passo 1

Fala, galerinha! Tranquilo?

A questão quer os momentos de inércia I x e I y e os raios de giração x - - e y - - do triângulo com vértices 0 ,   0 ,   b ,   0 ,   ( 0 ,   h ) . Para encontrar os momentos de inércia temos as seguintes integrais:

I x = ∬ D   y 2   ρ x ,   y   d A

I y = ∬ D   x 2   ρ x ,   y   d A

E os raios de giração são dados por:

x - - = I y m

y - - = I x m

Aqui temos a massa m da lâmina que podemos achar pela equação:

m = ρ   .   Á r e a   d a   l â m i n a

Então, precisamos achar nossos limites de integração através da descrição do nosso triângulo.

Daí é só resolvermos nossas integrais, que a gente faz de dentro pra fora integrando em relação a uma variável de cada vez e substituir os valores nas equações.

Vamos lá!

Passo 2

Vamos dedicar esse passo inicial à definição dos nossos limites de integração em x e y :

triângulo com vértices 0 ,   0 ,   b ,   0 ,   ( 0 ,   h )

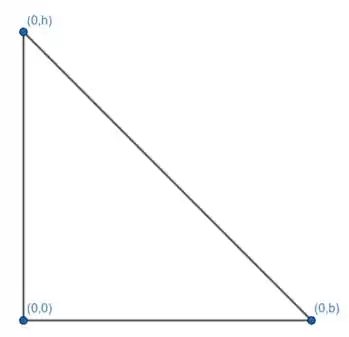
Vamos expressar essa região como uma região do Tipo I, onde x está entre duas constantes e y entre funções. Os valores de x variam assim:

0 ≤ x ≤ b

Os valores de y começam em 0 e vão até a reta que liga os pontos b ,   0 e ( 0 ,   h ) . Vamos determinar a equação da reta por dois pontos:

y = a x + b

Vamos calcular a inclinação a :

a = y 2 - y 1 x 2 - x 1

Substituindo:

a = h - 0 0 - b = - h b

O valor de b ocorro quando x = 0 , e nós já temos esse ponto: ( 0 ,   h ) . Substituindo na nossa equação, ficamos com:

y = h - h x b

Então a variação de y é:

0 ≤ y ≤ h - h x b

Passo 3

Galera, pra encontrar os momentos de inércia, vamos montar suas respectivas integrais, beleza?

I x = ∬ D   y 2   ρ x ,   y   d A

Colocando os limites de integração de cada variável:

= ∫ 0 b ∫ 0 h - h x b ρ y 2   d y   d x

Integrando primeiro em relação a y :

= ∫ 0 b ρ   y 3 3 0 h - h x b   d x

Aplicando os limites:

= ∫ 0 b ρ h - h x b 3 3   d x

Integrando finalmente em x :

= ρ 3 ∫ 0 b h - h x b 3   d x

Temos:

= ρ 3 h 3 x - 3 x 2 2 b + x 3 b 2 - x 4 4 b 3 0 b

Aplicando os limites de integração, ficamos com:

I x = ρ b h 3 12

Fazendo o mesmo processo para I y :

I y = ∬ D   x 2   ρ x ,   y   d A

Temos:

= ∫ 0 b ∫ 0 h - h x b ρ x 2   d y   d x

Integrando em y que é a integral de dentro, tratando x como constante:

= ∫ 0 b ρ x 2 y 0 h - h x b   d x

Aplicando os limites:

= ∫ 0 b ρ x 2 h - h x b   d x

Agora podemos finalmente integrar em x :

= ρ h x 3 3 - ρ h x 4 4 b 0 b

Aplicando os limites, temos por fim:

I y = ρ b 3 h 12

Passo 4

Pra encontrar os raios de giração, precisamos saber a massa da lâmina:

m = ρ   .   Á r e a   d a   l â m i n a

Como temos um triângulo, sua área é:

Á r e a   d a   l â m i n a = b ⋅ h 2

Então nossa massa fica:

m = ρ b h 2

Agora sim podemos determinar os raios de giração:

x - - = I y m

Substituindo os valores que encontramos:

= ρ b 3 h 12 ρ b h 2 = b 2 6

x - - = b 6

Agora para y - - :

y - - = I x m

Substituindo os valores que encontramos:

= ρ b h 3 12 ρ b h 2 = h 2 6

Então, teremos:

y - - = h 6

Resposta

I x = ρ b h 3 12

I y = ρ b 3 h 12

x - - = b 6

y - - = h 6

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Considere uma pá quadrada de um ventilador com lados de comprimento 2 e com o canto inferior esquerdo colocado na origem. Se a densidade da pá for ρ x ,y = 1 + 0,1 x , é mais difícil girar a pá em tor
Uma lâmina com densidade constante ρ x ,y = ρ ocupa a região dada. Encontre os momentos de inércia I x e I y e os raios de giração x - - e y - - .A parte do disco x 2 + y 2 ≤ a 2 no primeiro quadrante
Utilize um sistema de computação algébrica para determinar a massa, o centro de massa e os momentos de inércia da lâmina que ocupa a região D e tem a densidade dada. D é limitada pelo cardioide r = 1
Utilize um sistema de computação algébrica para determinar a massa, o centro de massa e os momentos de inércia da lâmina que ocupa a região D e tem a densidade dada. D = x ,y 0 ≤ y ≤ s e nx,0 ≤ x ≤ π