Enunciado
Cálculo - Diva Flemming - Cálculo B - Ed: 2º - Capítulo 10.11 - Ex. 42 - a
Uma lamina esférica é representada pela equação vetorial
- Supondo a = 4 , representar sobre a esfera as curvas coordenadas obtidas fixando e , respectivamente
- Determinar os vetores tangentes e , represente-os sobre a esfera
- Determinar o vetor , representando -o no corresponde ponto P
- Supondo que a densidade da esfera é constante. calcular o momento de inercia da esfera com relação ao eixo y
Passo 1
- Supondo a = 4 , representar sobre a esfera as curvas coordenadas obtidas fixando e , respectivamente
Fixando o ângulo Polar – o nosso – Faz com nosso ângulo Azimutal – o nosso – Varie ao longo da esfera, e isso nos da um circulo vertical
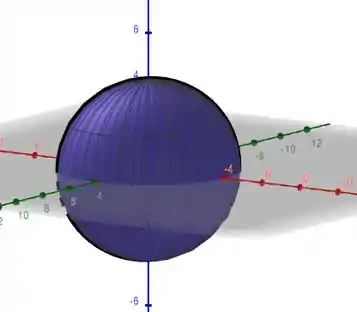
Agora se fixarmos o ângulo Azimutal, teremos um circulo paralelo ao plano XY – digamos um circulo na Horizontal.
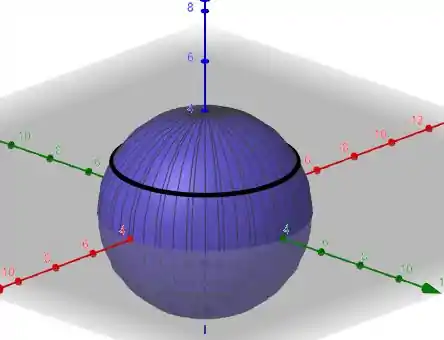
Terminamos por aqui. Te vejo na próxima resolução
: )
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
Calcule a integral de superfície. ∬ x z d S S é parte do plano 2 x + 2 y + z = 4 que está no primeiro octante.
Calcule a integral de superfície. ∬ ( x 2 z + y 2 z ) d S S é o hemisfério x 2 + y 2 + z 2 = 4 ,z ≥ 0 .
Calcule a integral de superfície. ∬ ( x + y + z ) d S S é a parte da metade do cilindro x 2 + z 2 = 1 ,z ≥ 0 , que está entre os planos y = 0 e y = 2 .
Calcule a integral de superfície. ∬ x 2 y z d S S é parte do plano z = 1 + 2 x + 3 y que está acima do retângulo 0,3 × [ 0,2 ] .
Calcule a integral de superfície. ∬ y 2 d S S é a parte da esfera x 2 + y 2 + z 2 = 1 que está acima do cone z = x 2 + y 2 .