Uma lâmina tem a forma da parte do plano recortada pelo cilindro Determine a massa dessa lamina se a densidade no ponto ( x,y,z) é proporcional à distancia desse ponto ao plano xy

Vamos encontrar as derivadas parciais de z

Assim

Vamos unir a integral

Vamos implantar agora nossa função

Quando projetamos o recorte do plano com o cilindro no plano XY obtermos essa região

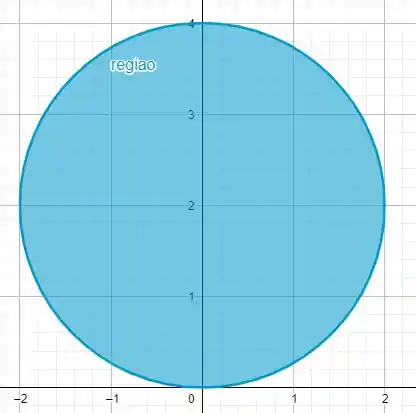
Primeira coisa a dizer. Essa região é muito ruim de integrar, porque ela está descentralizada dos eixos. Isso quer dizer que quando mudarmos para polar o nosso sera uma função do ângulo , ou seja, você vai pedir arrego no meio do exercício, porque ele ficaria imenso.

Então tenho uma super dica do meu professor de calculo 3. Vamos fazer uma mudança de espaço vamos sair dessa região cartesiana para uma cartesina*

Onde nessa nossa região cartesiana a nossa região esteja centralizada. Faremos assim

O melhor desse tipo de transformação é que o Jacobiano – A distorção espacial é 1. Porque não estamos distorcendo o espaço, apenas transladando. Então nossa região no fica

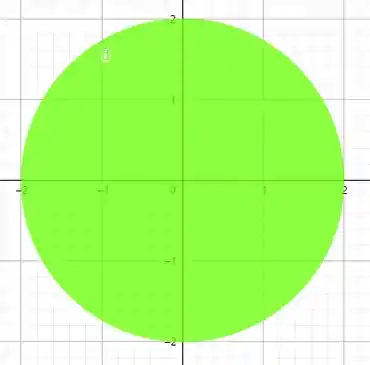
E assim nossa integral fica infinitamente mais fácil. Então tínhamos

E agora teremos

Já sabemos que estamos em um sistema de cartesiano transladado então vou voltar a usar apenas sem o *, certo? 😉

Vamos passar para polares agora 😉

DICA 2 : Quando integramos seno ou cosseno entre o resultado é zero. Entao para facilitar a gente podemos logo integrar em relação a

Terminamos por aqui. Te vejo na próxima resolução

: )