Uma lata de refrigerante morna é colocada na geladeira. Esboce o gráfico da temperatura do refrigerante como uma função do tempo. A taxa de variação inicial da temperatura é maior ou menor que a taxa de variação após hora?
Passo 1
Opa, vamo que vamo! Nessa questão temos que esboçar um gráfico da variação de temperatura de uma lata de refrigente morna que foi colocada na geladeira, em relação ao tempo!
Bem, se a gente coloca uma coisa morna na geladedeira ela gela, então a sua temperatura vai cair com o tempo e nosso gráfico vai ser decrescente!
-Mas gela quanto?
Como na geladeira existe um processo termodinâmico onde estamos sempre retirando calor, então desde o momento que a gente coloca a latinha na geladeira o sistema geladeira+latinha vai tender a um equilíbrio térmico.
Como latinha não gera calor e a geladeira tá sempre retirando calor da latinha podemos esperar que a temperatura de equilíbrio vai ser igual a temperatura da geladeira.
Fez sentido?!
Show, repara que eu disse que o sistema TENDE a um equilíbrio! Isso te lembra alguma coisa?!
Exatamente, se a temperatura tende a um valor fixo temos uma assíntota vertical em:
Vamos dizer que a temperatura inicial da latinha é de e da geladeira é de . Então vamos ter uma curva que sai do ponto:
E vai para:
Portanto a carinha do gráfico vai ser assim:
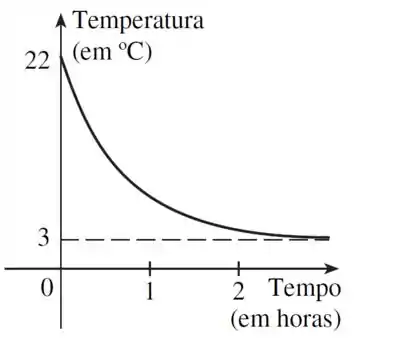
Passo 2
Aí o enunciado pergunta mais uma coisa! A taxa de variação inicial da temperatura é maior ou menor que a taxa de variação após hora?
A taxa de variação em um ponto é igual a inclinação da sua reta tangente. Comparando os pontos e vemos que a reta tangente inicial é mais ingrime.
Só que as duas taxas de inclinação são negativas, se a primeira é mais ingrime ela é mais negativa.
Portanto podemos dizer que a taxa de variação final é maior. Mas não é porque no final estamos trocando mais calor e sim porque estamos comparando duas taxas negativas!
Resposta
O esboço do gráfico é:
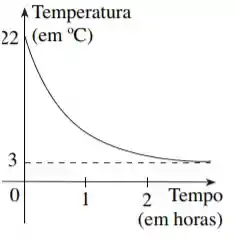
E a taxa de variação final é maior.