Enunciado
Cálculo - Cálculo Volume 1 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 1.5 - Ex. 14
Uma função f é dada por meio de uma descrição verbal. Determine se f é injetora.
é o tamanho do sapato que você calça com anos.
Passo 1
Fala galera!
Bom, para saber se uma função é injetora, vamos ver o conceito de função injetora. Uma função injetora é uma função que para cada valor no contradomínio existe apenas um valor no domínio associado.
Em palavras mais simples, dois não vão ter o mesmo .
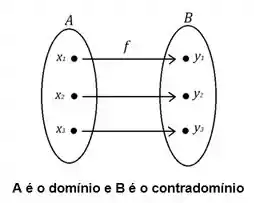
O método que usamos pra ver se uma função é injetora, é o método da reta horizontal. Se nós podemos traçar qualquer reta horizontal e ela cruzar a curva em mais de um ponto, então a função não é injetora.
Vamos então primeiro entender essa função que o enunciado comenta.
Passo 2
Agora vamos analisar a descrição da função f:
é o tamanho do sapato que você calça com anos
A tamanho do pé de uma pessoa aumenta até a sua vida adulta, quando ela para de crescer. Então pode ser algo mais ou menos assim:
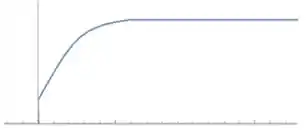
Ou seja, temos sim mais de um valor de (domínio) com o mesmo (contradomínio), em todo intervalo em que a função se torna constante.
E por isso, conseguimos traçar uma reta horizontal que passa pela curva mais de uma vez:
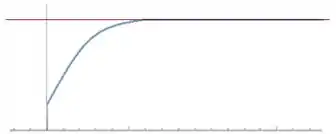
Uma função assim não é injetora!
Resposta
A função f não é injetora.