Enunciado
Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 4.5 - Ex. 32
Uma lata de sopa com forma de cilindro circular reto, raio e altura deve ter um volume . A tampa e a base são cortadas de quadrados, conforme a Figura Ex-32 a seguir. Se os cantos sombreados forem os únicos refugos, encontre a razão para a lata que requer menos material (incluindo o refugo).
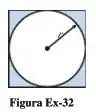
Passo 1
Então galera, a geometria do nosso problema é a seguinte: temos um cilindro circular reto no qual o topo e a base desse cilindro, ao invés de serem tampas circulares, são tampas quadradas. A área dessa lata de sopa é a somatória da área do cilindro e das áreas das tampas, ou seja:
Como a tampa é a mesma coisa que a tampa :
Ademais, o volume dessa lata de sopa é dado por:
Que é o produto entre a área da base e a altura do cilindro. Isolando , teremos:
Substituindo na expressão da área:
Passo 2
Como estamos procurando dimensões mínimas na fabricação da lata, então temos que utilizar a noção de máximos e mínimos, conforme aprendemos no cálculo! Derivando nossa expressão, teremos:
Igualando a zero:
Ok, encontramos um ponto crítico, mas como fazemos para provar que é, de fato, um mínimo? Vamos utilizar o conceito da derivada segunda, se liga:
Note que como é sempre positivo, então essa derivada segunda sempre será positiva, ou seja, a concavidade da função é para cima, o que indica um ponto de mínimo no que encontramos!
Passo 3
Como queremos encontrar a razão , basta substituirmos o que encontramos, se liga:
Como , então:
E essa é a razão necessária para a lata que requer menos material! 😊