Enunciado
Cálculo - Cálculo Volume 1 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 4.3 - Ex. 9
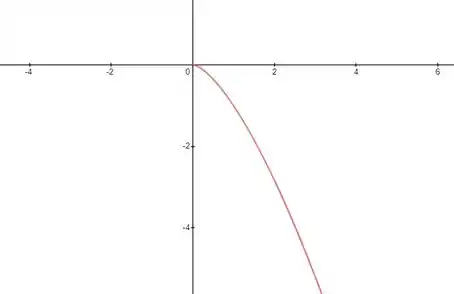
Esboce o gráfico de uma função com derivadas primeira e segunda sempre negativas.
Passo 1
Olá, meu querido e amado amigo. Yuri aqui e estarei te ajudando a resolver essa atividade.
Primeiramente, devemos lembrar o que significa para uma função ter sempre derivadas primeira e segunda negativas.
Temos o teste de Aumento/Diminuição (Seção 4.3), que afirma que se
para em algum intervalo , a função está diminuindo nesse intervalo.
Na mesma seção, temos o teste de Concavidade, que afirma que se para em algum intervalo , a função é côncava para baixo nesse intervalo.
Passo 2
Isso significa que precisamos esboçar o gráfico de uma função que sempre está diminuindo e sempre é côncava para baixo.
Assim, existem muitas soluções para este problema, uma delas sendo .
Se a primeira derivada é sempre negativa, isso quer dizer que nossa função é sempre decrescente.
A outro condição é que a segunda derivada também seja sempre negativa, isto é, nossa curva possui concavidade para cima. Então vamos lá esboçar uma gráfico!
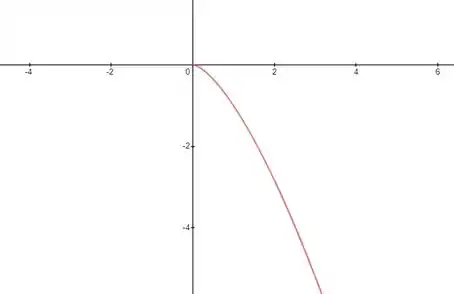
Resposta
