Enunciado
Cálculo - Cálculo Volume 1 - 7ª Edição - James Stewart- Ed: 7º - Capítulo 5.1 - Ex. 1 a
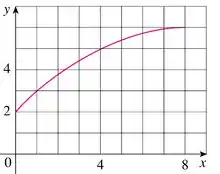
Lendo os valores do gráfico dado de utilize quatro retângulos para encontrar as estimativas inferior e superior para a área sob o gráfico dado de de ate Em cada caso, esboce os retângulos que você usar.
Passo 1
Fala, galera! Beleza?
O enunciado pediu pra gente encontrar as estimativas inferior e superior para a área sob o gráfico de no intervalo de até , utilizando retângulos.
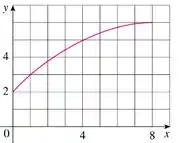
Tem ideia de como fazemos isso?
Pra isso, vamos relembrar que as estimativas superiores e inferiores, em um intervalo são obtidas através da soma:
Onde e .
Como já foi dado o intervalo, temos que e E como é crescente podemos obter uma estimativa inferior usando os pontos da esquerda e os pontos da direita para obter a estimativa superior.
Nós fomos instruídos a usar 4 retângulos, então e como , temos que:
Vamos lá!
Passo 2
Vamos começar pela estimativa inferior...
Vamos definir pelos valores à esquerda dos retângulos das áreas.
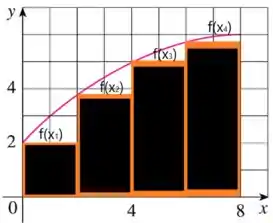
Aplicando o somatório que vimos no passo 1, temos:
Como estamos fazendo a estimativa inferior, temos que , , e .
Analisando o gráfico, podemos definir as imagens de nesses pontos como
Tranquilo até aqui?
Passo 3
Agora vamos fazer pela estimativa superior alinhando os retângulos pela direita da função...
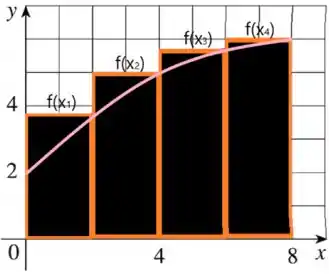
Aplicando o somatório do passo 1:
Nesse caso, como nosso alinhamento acontece pela direita, temos: , , e .
Observando o gráfico, podemos estimar as imagens de como:
É isso! O que achou? Responde Aí!