Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 9.2 - Ex. 5
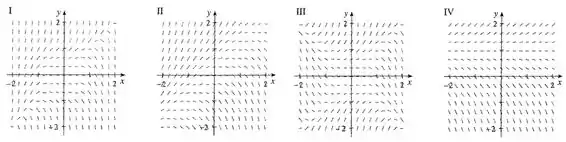
Ligue a equação diferencial a seu campo de direções (I-IV). Dê razões para sua resposta.
Passo 1
O problema pede para acharmos o campo de direções da equação diferencial
Para resolver esse problema, temos que lembrar que da a inclinação das soluções em cada ponto. Assim, onde , as curvas serão crescentes, e o contrário ocorre para . Além disso, onde as direções do campo são horizontais!
Temos que se . Na figura a seguir desenhamos essas duas retas e os sinais de em cada região:
Para cima e para baixo da fronteira desenhada as curvas serão crescentes, mas nas laterais serão decrescentes!
O único gráfico que contempla essas propriedades é o III.
Resposta
III
Exercícios de Livros Relacionados
Use o Campo de Direções I acima para esboçar os gráficos das soluções que satisfazem as condições iniciais dadas
Use o método de Euler com o passo 0,2 para estimar y ( 0,6 ) , onde y ( x ) é a solução do problema de valor inicial y ' = cos x + y y 0 = 0
Use o método de Euler com o passo 0,2 para estimar y ( 1 ) , onde y ( x ) é a solução do problema de valor inicial y ' = x 2 y - 1 2 y 2 y 0 = 1
The Fitzhugh-Nagumo model for the electrical impulse in a neuron states that, in the absence of relaxation effects, the electrical potential in a neuron v t obeys the differential equation d v d t =-
Use a computer algebra system to draw a direction field for the given differential equation. Get a printout and sketch on it the solution curve that passes through (0, 1). Then use the CAS to draw the