Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.2 - Ex. 3
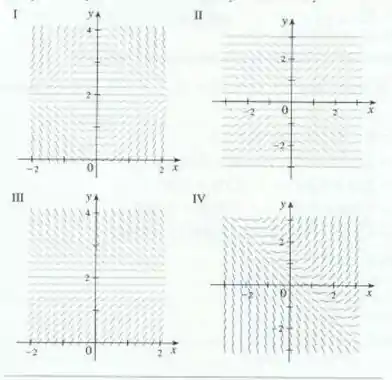
Ligue a equação diferencial a seu campo de direções (I – IV). Dê as razões para sua resposta.
3.
Passo 1
Precisamos encontrar qual dos campos de direção apresentados corresponde a equação .
Podemos começar analisando o que acontece quando . Nesse ponto , portanto existe uma linha horizontal em . Essa situação acontece em I e III apenas.
Passo 2
Agora podemos pensar o que acontece quando . Nesse ponto , ou seja, a reta tangente nesse ponto tem uma inclinação positiva igual a . Ao olharmos para nossas opções de campos (I e III), vemos que a única solução possível é III, pois em I quando .
Resposta
3. III
Exercícios de Livros Relacionados
Ache a solução completa para a equação diferencial: x 2 d y d x + 2 x y = e x
Ache a solução completa para a equação diferencial: d y d x = y 2 x + y 4
Ache a solução completa para a equação diferencial: d y d x + 2 y cotg x = cos x
Ache a solução completa para a equação diferencial: 2 y d y d x = 1 e y 2 + x
Ache uma solução da equação diferencial que satisfaça a condição dada. d y d x + y tg x = sec x ; y = 1 quando x = 0 .