Enunciado
Cálculo - Cálculo Volume 2 - 8ª Edição - James Stewart- Ed: 8º - Capítulo 9.2 - Ex. 5
Ligue a equação diferencial a seu campo de direções (I – IV). Dê as razões para sua resposta.
5.
Passo 1
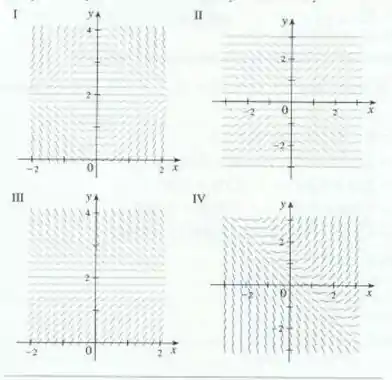
Precisamos encontrar qual dos campos de direção apresentados corresponde a equação Podemos começar analisando quando . Nesse caso . O campo direcional IV satisfaz essa condição. Note que na reta nós temos , o que é verdade em IV.
Resposta
5. IV
Exercícios de Livros Relacionados
Resolva a equação diferencial por dois métodos:a)Use um fator de integração d y d x + y x = 0
Resolva a equação diferencial por dois métodos:b)Separe as variáveis. d y d x + y cos x = 0
Resolva a equação diferencial por dois métodos:a)Use um fator de integração d y d x + y tg x = 0
Resolva a equação diferencial por dois métodos:a)Use um fator de integração d y d x + y cos x = 0
Resolva a equação diferencial por dois métodos:Separe as variáveis. x + 1 x d y d x + y = 0