Enunciado
Cálculo - Cálculo Volume 2 - 5ª Edição - James Stewart- Ed: 5º - Capítulo 10.3 - Ex. 40
Esboce a curva com equação dada.
Passo 1
O problema pede para esboçarmos a curva em coordenadas polares. A gente vai analisar essa curva em intervalos a partir das informações encontradas no seu gráfico cartesiano.
Para gerarmos o gráfico cartesiano da curva, iremos utilizar o GeoGebra, para gerar o gráfico polar, iremos utilizar o Desmos.
O primeiro passo é esboçar como função de em coordenadas cartesianas:
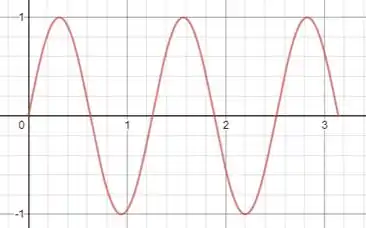
No intervalo de , a curva começa na origem, conforme o ângulo aumenta ela se afasta e depois passa a retornar até chegar novamente na origem:
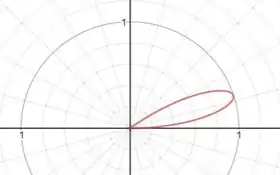
Passo 2
No intervalo seguinte, , é negativo, de modo que rebatemos o laço para o quadrante oposto:
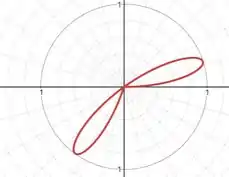
No próximo intervalo, volta a ser positivo:
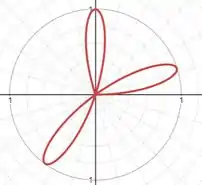
Nos dois intervalores seguintes será negativo e positivo, respectivamente, sempre executando a mesma oscilação e completando o ciclo:
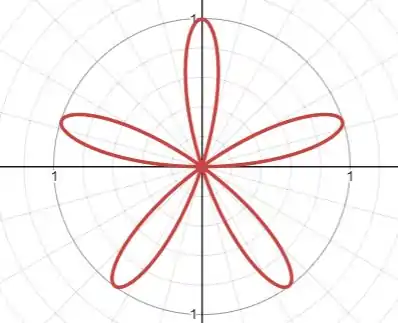
Resposta
Esboço.